Advances along Adversarial Training - 2

By LI Haoyang 2020.11.16

Content

The prevailing defense method is called adversarial training. Theoretically, a min-max optimization is formulated with the idea of adversarial training to train a robust model,i.e. adversarial training, aiming to solve the following problem:

The inner formulation searches an optimal perturbation in allowed perturbations $\cal{S}$ and the outer formulation searches an optimal parameter $\theta$ to minimize the loss function respect to the perturbed example.

Adversarial Logit Pairing

Evaluating and Understanding the Robustness of Adversarial Logit Pairing - NIPS workshop 2018

Logan Engstrom, Andrew Ilyas, Anish Athalye. Evaluating and Understanding the Robustness of Adversarial Logit Pairing. NIPS SECML 2018. arXiv:1807.10272

We find that a network trained with Adversarial Logit Pairing achieves 0.6% correct classification rate under targeted adversarial attack, the threat model in which the defense is considered.

Basically, this paper dismissed the effectiveness of adversarial logit pairing....

Adversarial Logit Pairing

In Kannan et al., the authors claim that the defense of Madry et al. is ineffective when scaled to an ImageNet [Deng et al., 2009] classifier, and propose a new defense: Adversarial Logit Pairing (ALP).

ALP enforces the model to predict similar logit activations on unperturbed and adversarial versions of the same image, i.e. optimizing the loss

where $D$ is a distance function, $f$ is the neural network before the last layer (i.e. the part that produces logits) and $\lambda$ is a hyperparameter.

This objective is intended to promote “better internal representations of the data” [Kannan et al.] by providing an extra regularization term.

It's a penultimate version of adversarial training.

Evaluation

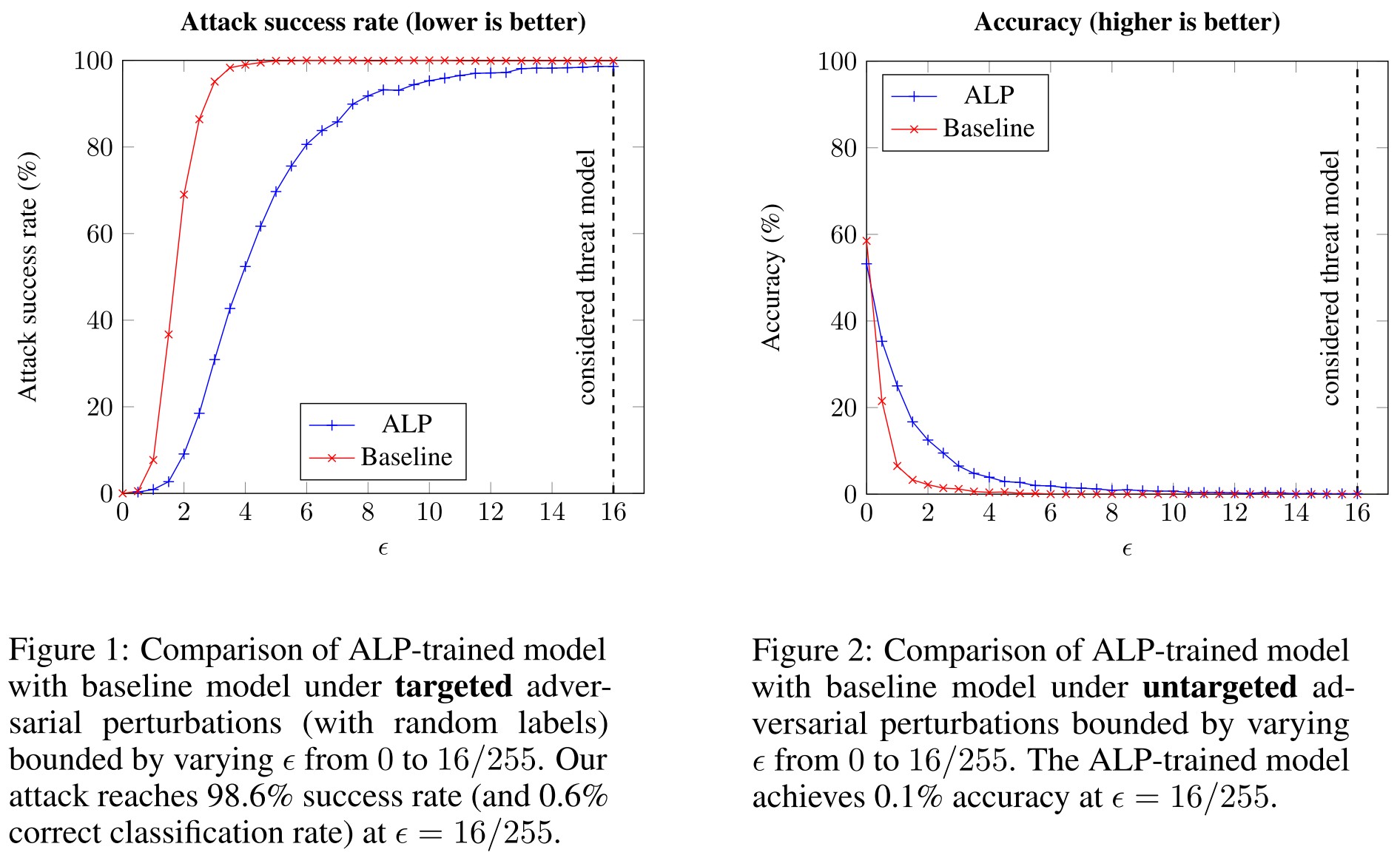
They show that ALP trained model is not as robust as claimed.

We originally used the evaluation code provided by the ALP authors and found that setting the number of steps in the PGD attack to 100 from the default of 20 significantly degrades accuracy. For ease of use we reimplemented a standard PGD attack, which we ran for up to 1000 steps or until convergence.

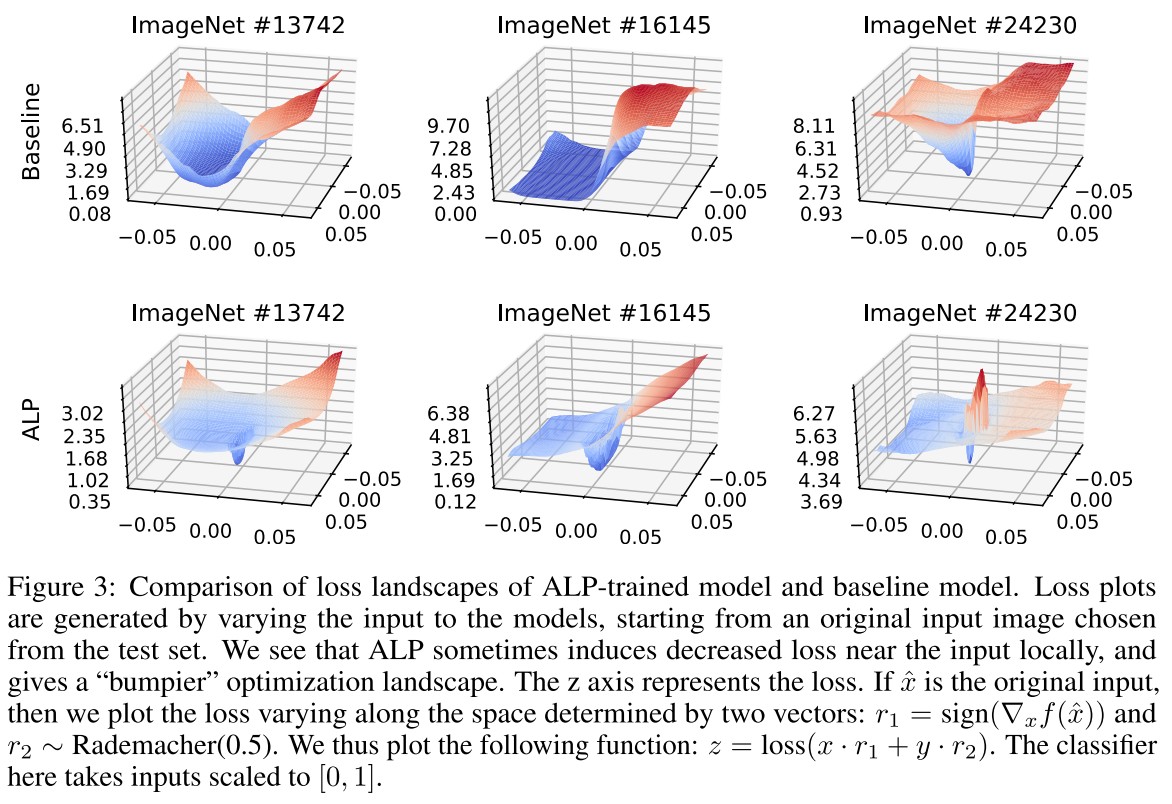
They also plot a loss landscape, showing that

The plots provide evidence that ALP sometimes induces a “bumpier,” depressed loss landscape tightly around the input points.

Evidence of potential gradient masking.

Inspiration

In this work, we perform an evaluation of the robustness of the Adversarial Logit Pairing defense (ALP) as proposed in Kannan et al., and show that it is not robust under the considered threat model.

They evaluate the adversarial logit pairing and show that it's not as robust as claimed.

Adversarial Training

Iterative Adversarial Training - 2020

Code: https://github.com/rohban-lab/Shaeiri_submitted_2020

Amirreza Shaeiri, Rozhin Nobahari, Mohammad Hossein Rohban. Towards Deep Learning Models Resistant to Large Perturbations. arXiv preprint 2020. arXiv:2003.13370

They discover that adversarial training with large perturbations directly fails and further propose to use the final weights of an adversarially trained model with small perturbations to initialize the model and iterative adversarial training (gradually increase the scale of perturbations) as an alternative.

Adversarial Training with Larger Perturbations

Starting from adversarial training

with the set of feasible perturbations as

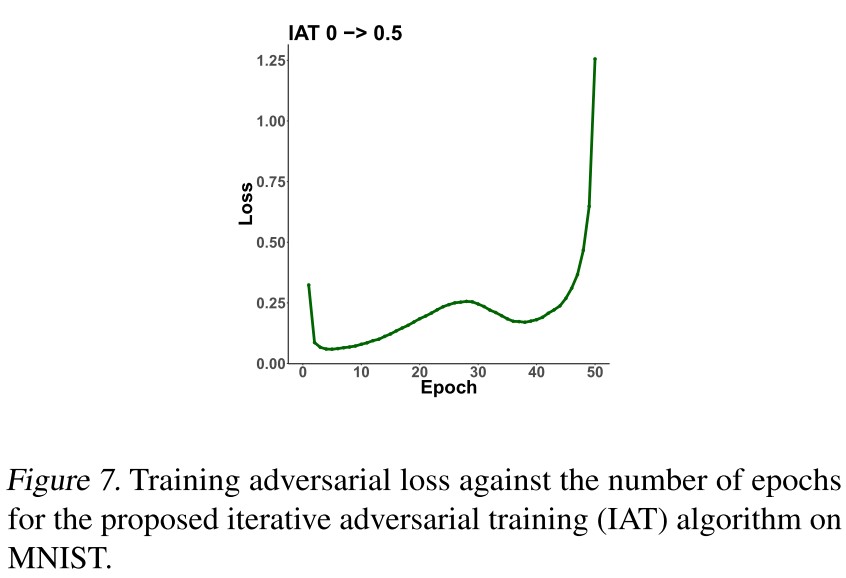
they observe that adversarial training on larger epsilons can not decrease the adversarial loss sufficiently, even on the training data.

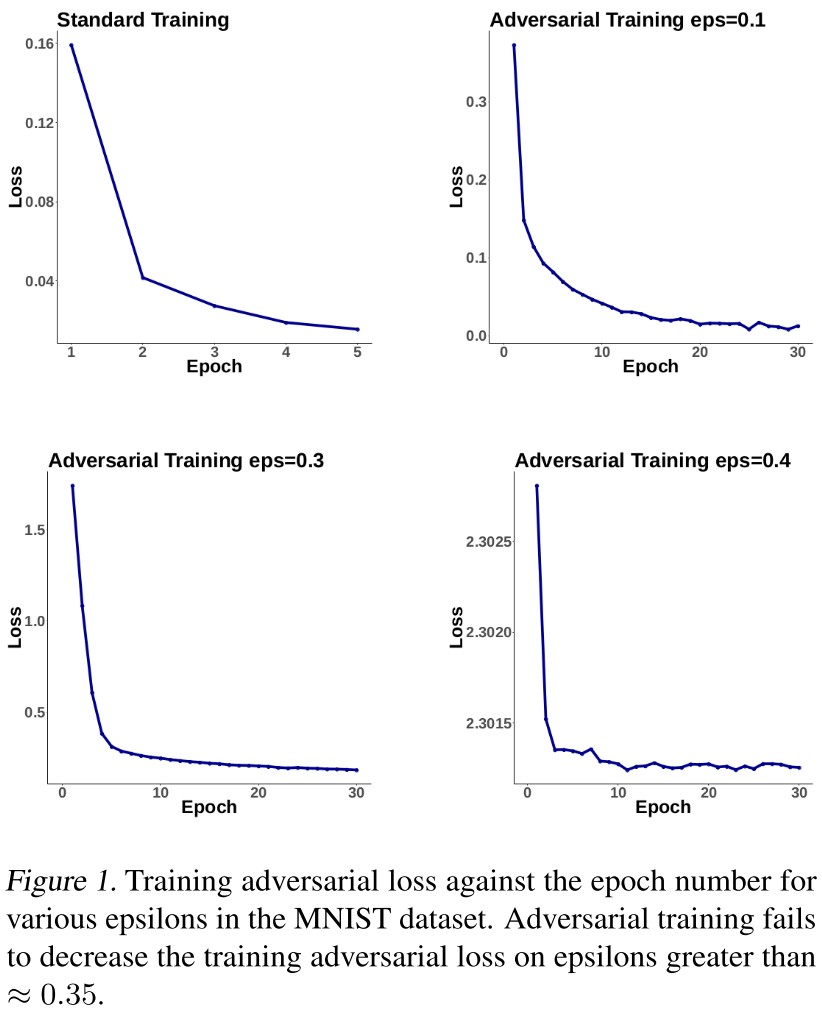
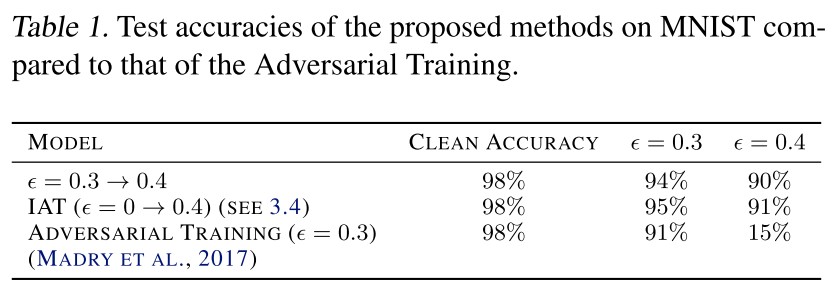
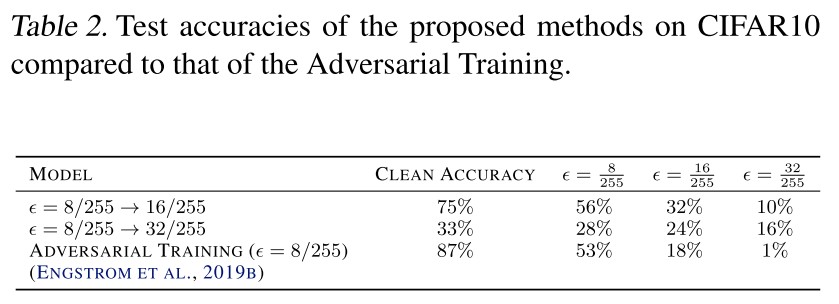
When we try to apply adversarial training on large epsilons, the training loss does not decrease.

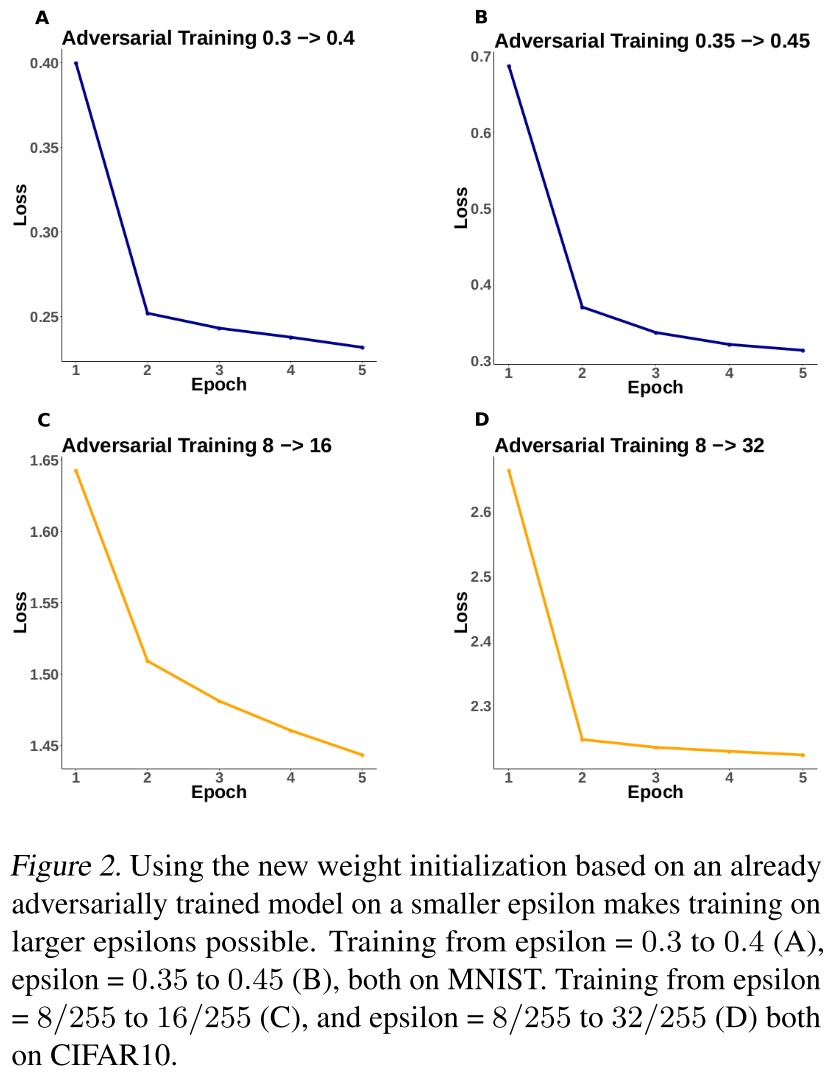
We take the weights from an adversarially trained model on epsilon = 0.3 in MNIST and epsilon = 8/255 in CIFAR10 as the initial weights, followed by adversarial training on larger epsilons.

This initialization makes the adversarial learning possible on larger epsilons in both datasets.

This discovery is actually not surprising, since a weak classifier is intuitively going to be broken by a very strong adversary, similarly as observed in the training of GAN.

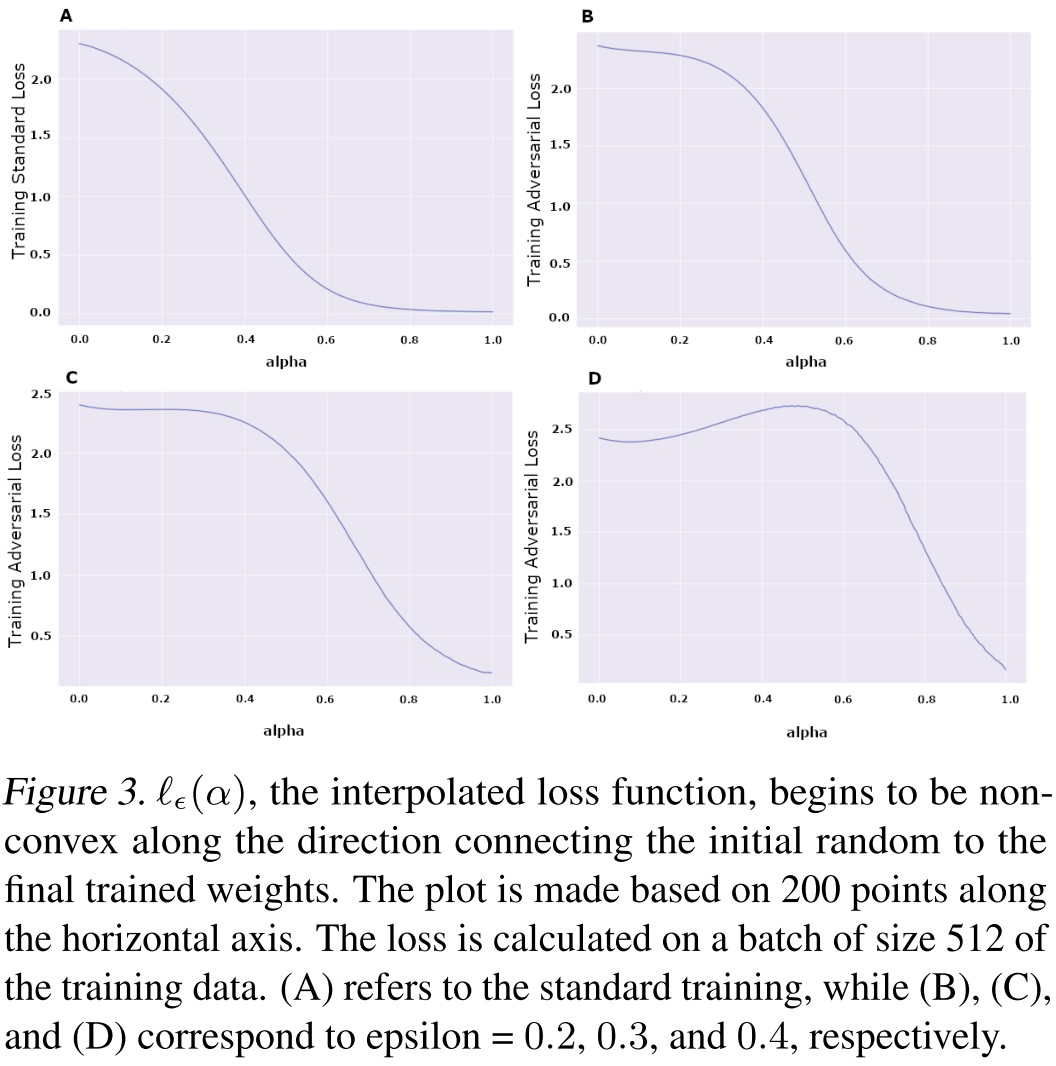
They further visualize the loss functions and observe that the loss function is convex for small perturbations but begins to be non-convex as epsilon grows (as shown in Figure 3).

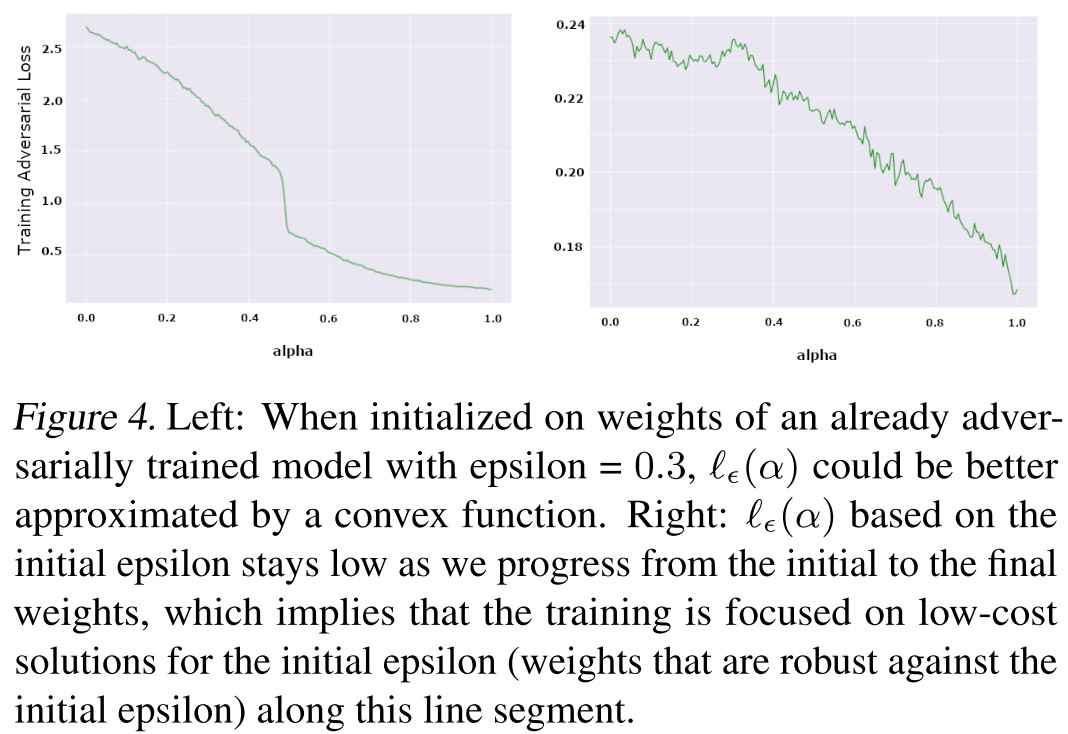
With the initial weights obtained from an adversarially trained model, the loss function seems to be well approximated by a convex function (as shown in Figure 4 (left)).

The given plot suggests that the proposed initialization makes the adversarial training focused on a small weight subspace. (as shown in Figure 4 (right)).

This suggests “mode connectivity” in our training and therefore, we could expect the optimization to converge quickly.

Iterative Adversarial Training

In IAT, the epsilon is gradually increased from 0 to the target epsilon with a specific schedule across epochs during the training.

Interpretability brought by adversarial training with large perturbations

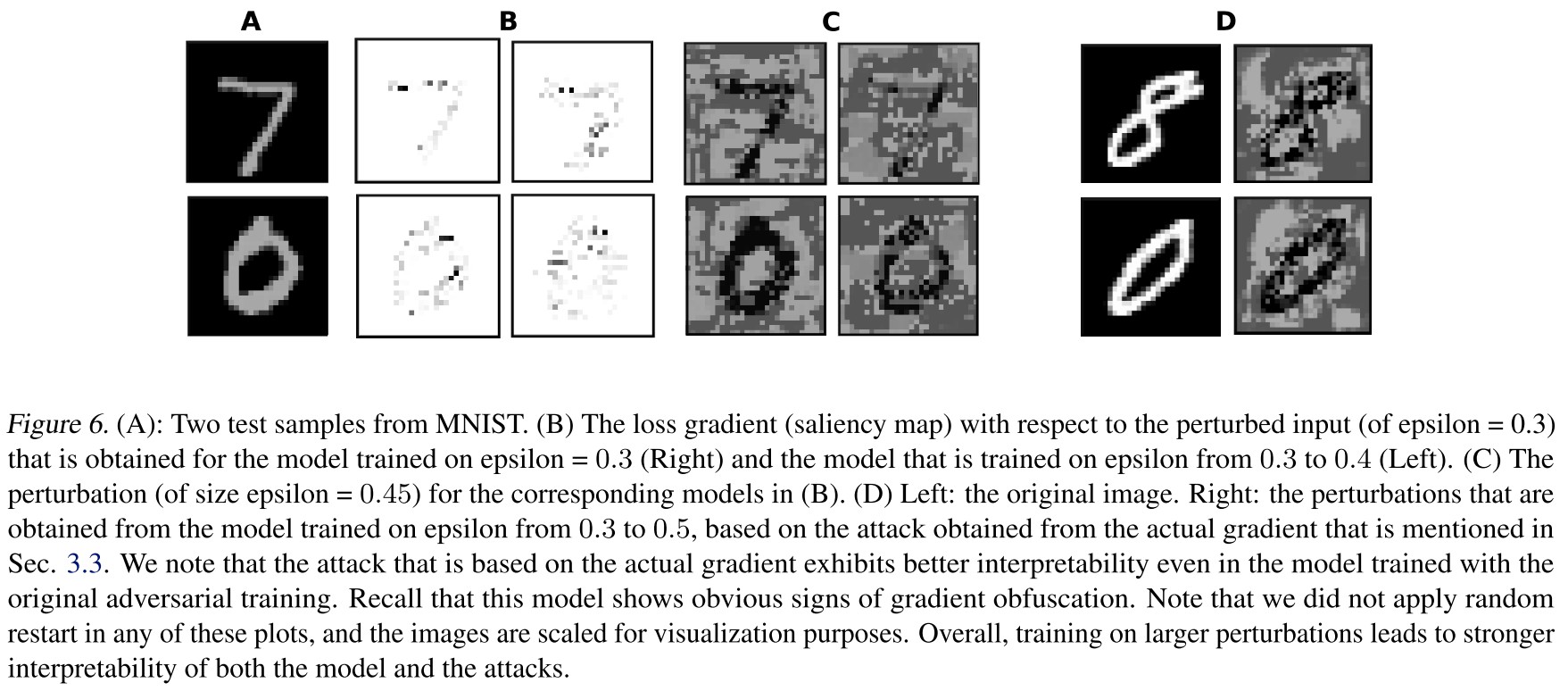
Specifically, we observe that the saliency map that is obtained from the loss gradient with respect to the input, evaluated on the perturbed data, in the model trained on larger epsilon, becomes more compact and concentrated around the foreground.

Similar conclusion have been made by Tsipras et al.

Theoretical Results

They also give some theoretical analysis, but I am not very intrigued, hence only a few is listed here.

Theorem 1 The problem of finding the optimal robust classifier given the joint data and label distribution $D(x,y)$ for the perturbations as large as $\epsilon$ in $\ell_p$ norm, is an $\mathcal{NP}$-hard problem.

Inspirations

This paper is not very interesting. Robustness against large perturbations are important without any doubt, the proposed method is also effective given the experiments provided, but the method is not very inspiring.