Adversarial Label Smoothing and Logit Squeezing

By LI Haoyang 2020.12.18 (branched)

Content

Adversarial Label Smoothing

Label Smoothing and Logit Squeezing - 2019

ICLR 2019 withdrawal

Ali Shafahi, Amin Ghiasi, Furong Huang, Tom Goldstein. Label Smoothing and Logit Squeezing: A Replacement for Adversarial Training? arXiv preprint 2019. arXiv:1910.11585

The method is interesting, although reviewers have criticized it by providing evidences that gradient masking may have occurred.

Be a critical reader when coping with a withdrawal work.

They empirically discover that the mechanism of adversarial training can be mimicked by label smoothing and logit squeezing, and

Remarkably, using these simple regularization methods in combination with Gaussian noise injection, we are able to achieve strong adversarial robustness – often exceeding that of adversarial training – using no adversarial examples.

What does Adversarial Training do?

At first glance, it seems that adversarial training might work by producing a large “logit gap,” i.e., by producing a logit for the true class that is much larger than the logit of other classes.

Surprisingly, adversarial training has the opposite effect – we will see below that it decreases the logit gap.

Consider an image $x$ with logit representation $z$ produced by a neural network. Let $z_y$ denote the logit corresponding to the correct class $y$.

Adding a small perturbation $\delta$ to $x$, the corresponding change in logits is approximately $\delta^\top\nabla_x z_y$ using a linear approximation.

A classifier is susceptible to adversarial perturbation $\delta$ if the perturbed logit of the true class is smaller than the perturbed logit of any other class, i.e.

A one-step attack with a $\ell_{\infty}$ step of $\epsilon_L$ such as FGSM approximates the perturbation by

Using this approximation, the equation becomes

Hence the smallest $\ell_{\infty}$-norm of the perturbation required is the ratio of "logit gap" to "gradient gap", i.e.

As shown in Table 1, this equation aligns with experiments.

Maximal robustness occurs when $\epsilon_L$ is as large as possible, therefore, by equation (4), there are three strategies:

• Increase the logit gap

  Maximize the numerator of equation 4 by producing a classifier with relatively large $z_y$.

• Squash the adversarial gradients

  Train a classifier that has small adversarial gradients $\nabla_x z_{\tilde{y}}$ for any class $\tilde{y}$. In this case a large perturbation is needed to significantly change $z_{\tilde{y}}$.

  The original defenses work by this strategy.

• Maximize gradient coherence

  Produce adversarial gradients $\nabla_x z_{\tilde{y}}$ that are highly correlated with the gradient for the correct class $\nabla_ x z_y$.

  In this case, one cannot decrease $z_y$ without also decreasing $z_{\tilde{y}}$, and so large perturbations are needed to change the class label.

Remarkably, our experimental investigation reveals that adversarial training does not rely on this strategy at all, but rather it decreases the logit gap and gradient gap simultaneously.

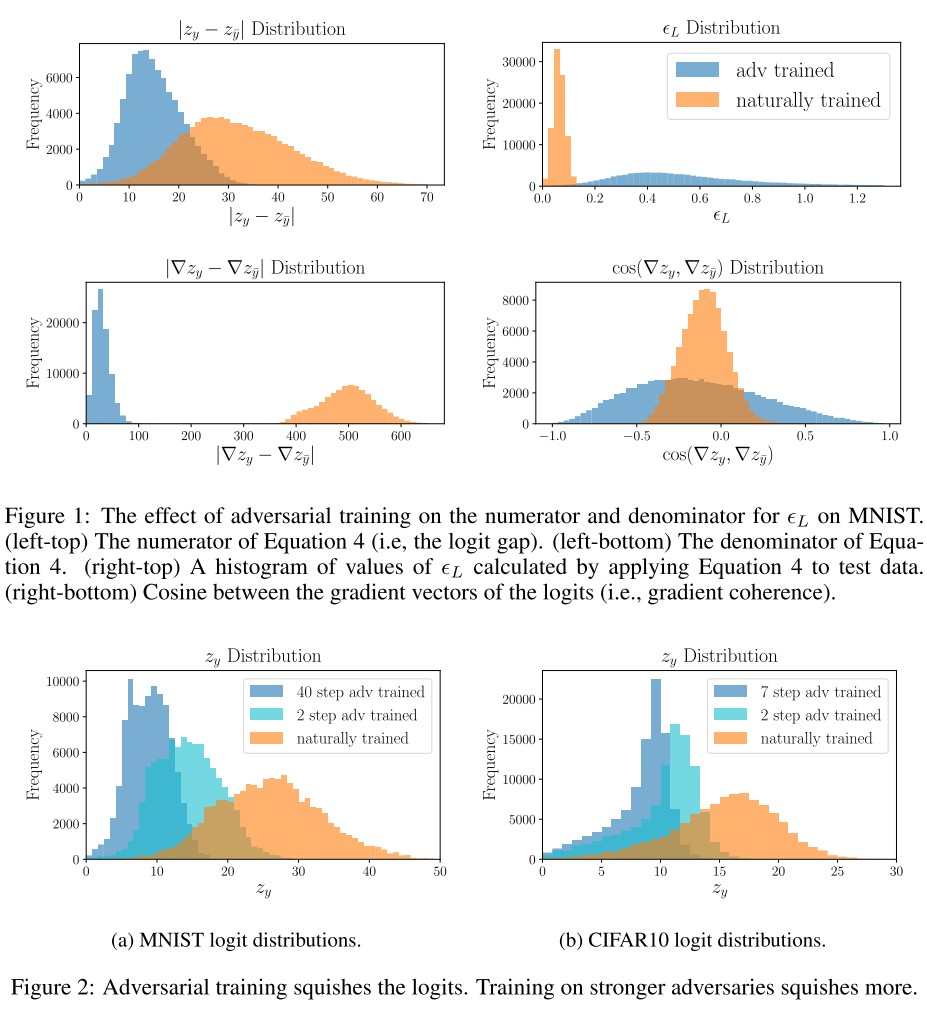
As shown in Figure 2:

Adversarial training succeeds by minimizing the denominator in Equation 4; it simultaneously squeezes the logits and crushes the adversarial gradients.

And then there is their motivation:

This leads us to ask an important question: If we directly decrease the logit gap, or the logits themselves, using an explicit regularization term, will this have the desired effect of crushing the adversarial gradients?

This explanation only works for small perturbations, the linear approximation is unlikely to work in a more complex situation.

Label Smoothing and Logit Squeezing

Label smoothing refers to converting "one-hot" label vectors into "one-warm" vectors, which encourages the classifier to produce small logit gaps.

A one-hot label vector $y_{hot}$ is smoothed by

where $\alpha\in[0,1]$ is the smoothing parameter and $N_c$ is the number of classes.

Logit squeezing refers to directly squashing all logit values by adding an explicit regularization term, i.e.

where $\beta$ is the squeezing parameter and $||\cdot||_F$ is the Frobenius norm of the logits for the mini-batch.

Our experimental results suggest that simple regularizers can hurt adversarial robustness, which agrees with the findings in Zantedeschi et al. (2017). However, these strategies become highly effective when combined with a simple trick from the adversarial training literature — data augmentation with Gaussian noise.

This is a little contradictory, above they state that increasing the logit gap should increase adversarial robustness and here they try to mimic adversarial training by squeezing the logit gap....

Gaussian Noise Save the Day

Label smoothing and logit squeezing become shockingly effective at hardening networks when they are combined with Gaussian noise augmentation.

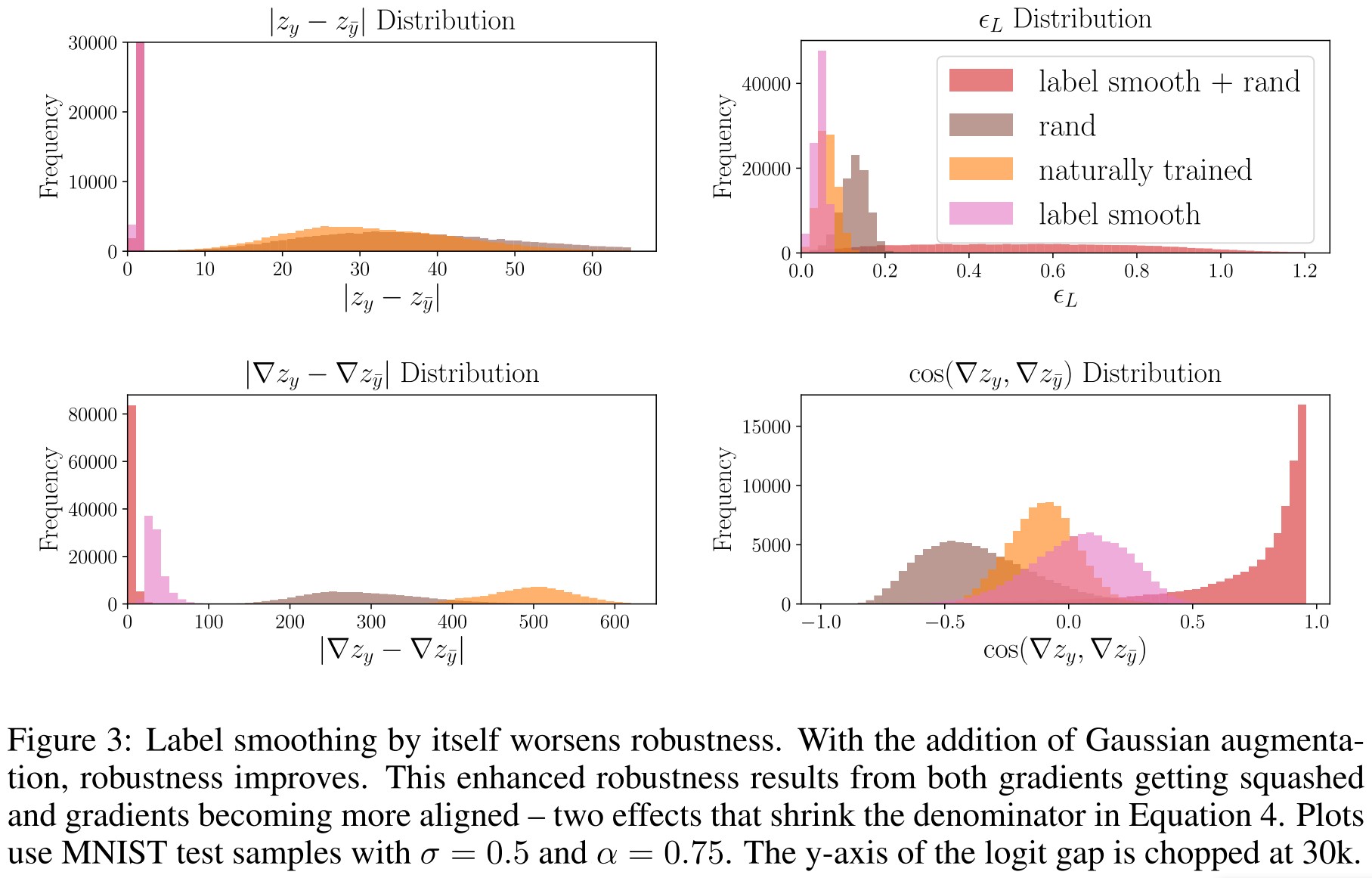
We also see that label smoothing alone causes a very slight drop in robustness; the shrink in the gradient gap is completely offset by a collapse in the logit gap.

Surprisingly, Gaussian noise and label smoothing have a powerful synergistic effect. When used together they cause a dramatic drop in the gradient gap, leading to a surge in robustness.

Comparison between Label Smoothing and Logit Squeezing

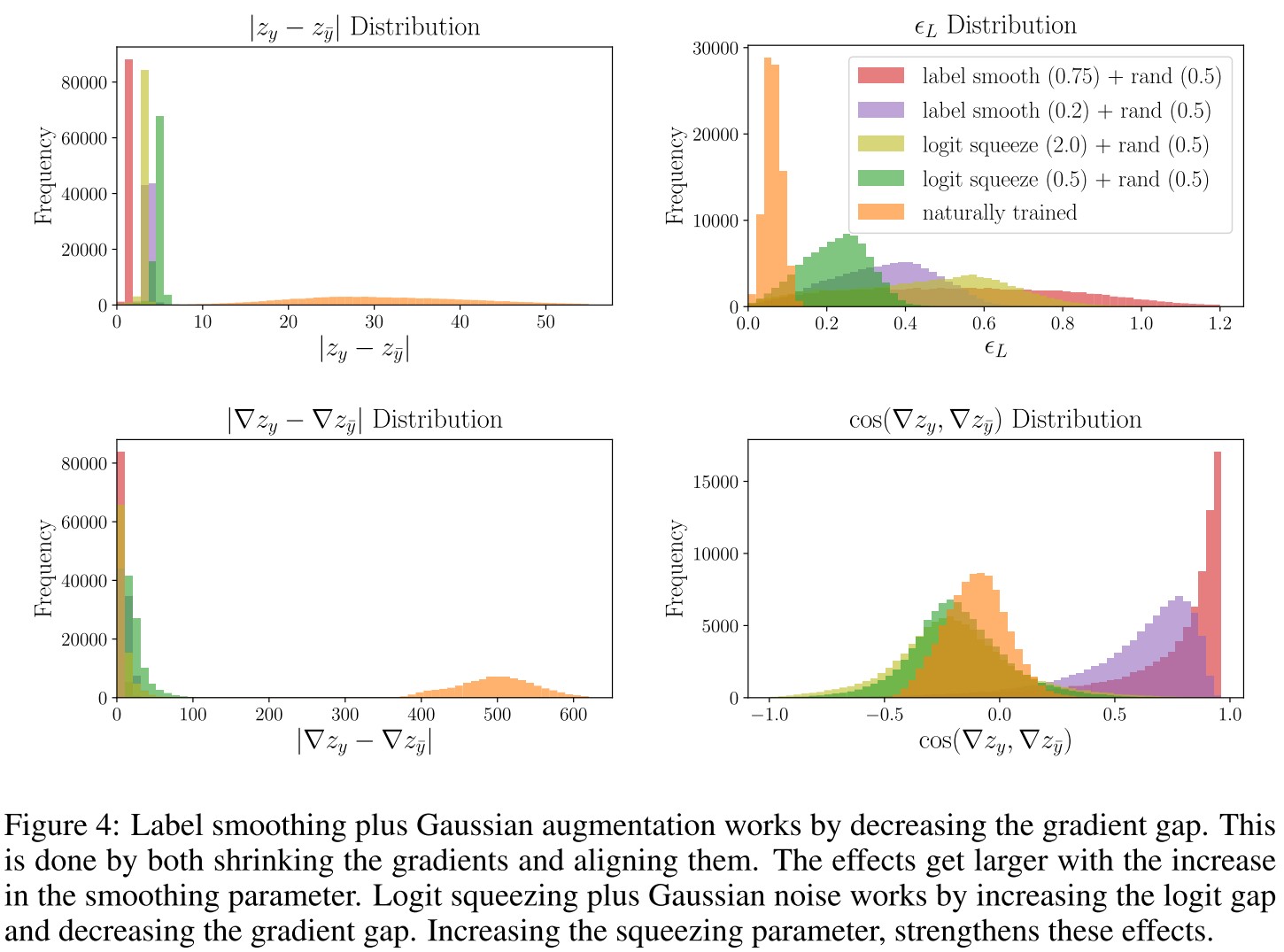
Label smoothing (i.e. reducing the variance of the logits) is helpful because it causes the gradient gap to decrease.

As shown in Figure 4:

We see that in label smoothing (with Gaussian augmentation), both the gradient magnitude decreases and the gradients get more aligned.

When logit squeezing is used with Gaussian augmentation, the magnitudes of the gradients decrease. The distribution of the cosines between gradients widens, but does not increase like it did for label smoothing.

Simultaneously increasing the numerator and decreasing the denominator of Equation 4 potentially gives a slight advantage to logit squeezing.

A fair explanation for the robustness gained by combining LS and Gaussian augmentation.

Experiments

We trained Wide-Resnet CIFAR-10 classifiers (depth=28 and k=10 ) using aggressive values for the smoothing and squeezing parameters on the CIFAR10 data set.

Keeping in mind that each step requires a forward and backward pass, the running time of training for 80,000 iterations on 7-step PDG examples is equivalent to 640,000 iterations of training with label smoothing or logit squeezing.

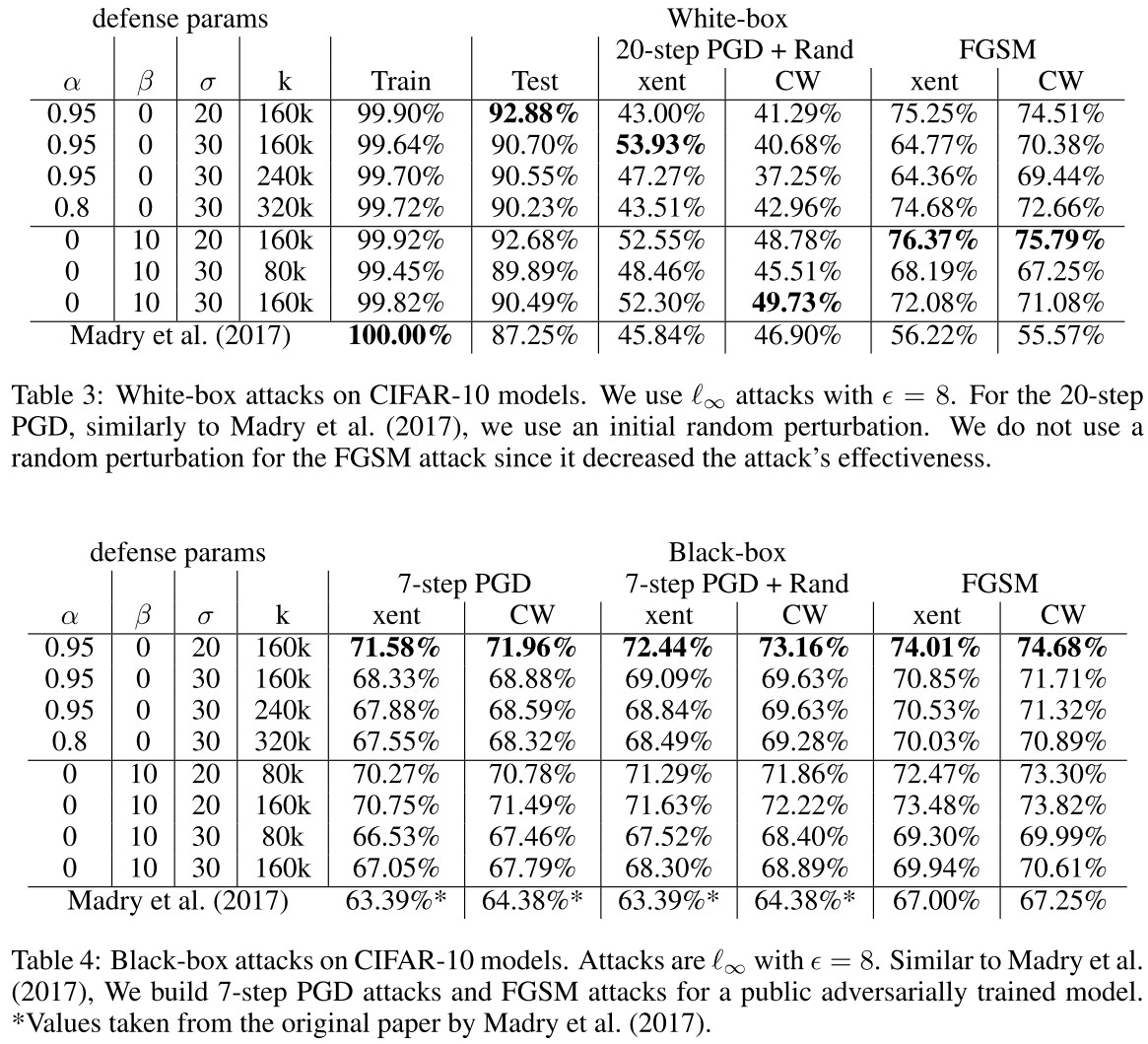
As shown in Table 4, with this aggressive LS augmented with Gaussian noise, the clean accuracy and robust accuracy both surpass naive adversarial training.

Although the results are challenged by reviewers....

They also perform a sanity check for gradient masking and show that the robustness is not gained by gradient masking.

Inspirations

The theoretical analysis on the logits is impressive and well classifies the existing strategies, and they also give a soundly explained defense in replacement of the expensive adversarial training.

Increasing the logit gap and decreasing the misalignment of gradients surely will increase robustness when the linear approximation holds for attacks as analyzed, but it's not that universal like adversarial training.

It seems that this painful solution will stand for a long time....

This paper is not perfect, but the reviewers were treating this paper unfairly and over confidently, one of them even omitted the most important analysis of authors and strongly reject this paper based on his prior beliefs.

Adversarial Robustness via Label-Smoothing - 2019

AISTATS 2020？

Morgane Goibert, Elvis Dohmatob. Adversarial Robustness via Label-Smoothing. arXiv preprint 2019. arXiv:1906.11567

They propose to use label-smoothing to increase adversarial robustness

The proposed Label-Smoothing methods have two main advantages: they can be implemented as a modified cross-entropy loss, thus do not require any modifications of the network architecture nor do they lead to increased training times, and they improve both standard and adversarial accuracy.

Unified framework for Label Smoothing

Precisely, LS withdraws a fraction of probability mass from the "true" class label and reallocates it to other classes.

Let the Total-Variation distance between two probability vectors $q^\prime,q\in\Delta_K$ be:

Half of the $L_1$ norm distance between these two probability vectors.

For $\alpha\in[0,1]$, define the uncertainty set of acceptable label distributions by

where:

• $\Delta_K:=\{q\in\R^K|q\ge 0,\sum_{k=1}^K q_k=1\}$, the $(K-1)$-dimensional probability simplex
• $\hat{Q}_{X,Y}^n\in\mathcal{P}(\mathcal{X}\times\mathcal{Y})$ is the joint distributions on the dataset $S_n$
• $q_i:=\hat{Q}_{Y|X=x_i}^n\in\Delta_K$ is a conditional label distribution within TV distance less than $\alpha$ with the one-hot coded label $y_i$.

By direct computation, there is

I think it's $1-(1/2)q_i^{(y_i)}$.

The uncertainty set can be rewritten as

Any conditional label distribution $q_i$ drawn from the uncertainty set can be written as

where the bold $\bold{y}_i$ denotes the one-hot coding.

Different choices of the probability vector $q_i^\prime$ then lead to different Label-Smoothing methods.

The general training of a NN with label smoothing then corresponds to the following optimization problem:

A cross-entropy loss weighted with uncertainty.

This optimization can be rewritten as the optimization of a usual cross-entropy loss plus a penalty term on the gap between the components of logits produced by the model on each example $x_i$.

Theorem 1 (General Label-Smoothing Formulation) The optimization problem is equivalent to the logit regularized problem

where $L_n(\theta):=-\frac{1}{n}\sum_{i=1}^n\log(p(x_i;\theta))$ is the standard cross-entropy loss and

where $z_i:=z(x_i;\theta)\in\R^K$ is the logits vector for $x_i$.

The extra term requires the logits vector for $x_i$ to mimic the difference of the one-hot coding between the uncertainty distribution. ?

Adversarial Label-Smoothing

It consider the worst possible smooth label $q_i$ for each example $x_i$, i.e.

The inner problem find the worst smooth label, and the outer problem minimizes on the worst smooth label.

The inner problem has an analytic solution, i.e.

where $y_i^{\text{worst}}\in\arg\min_{k=1}^K z^{(k)}(x_i,\theta)$ is the index of the smallest component of the logits vector $z_i$ for input $x_i$ and $\bold{y}_i^{\text{worst}}$ is the corresponding one-hot encoding.

Distribute some energy on the least likely label and train on it? It sounds ridiculous....

Apply Theorem 1, there is

Corollary 1 (ALS enforces logit-squeezing). The logit-regularized problem equivalent of the ALS problem is given by:

where:

For each data point $x_i$ with true label $y_i$, the logit squeezing penalty term $R_n(\theta)$ forces the model to refrain from making over-confident predictions.

It enforces that the difference between $1/n$ of the correct prediction and the least likely prediction should be small.

This means that every class label receives a positive prediction output probability, i.e.

One can also see ALS as the label analog of adversarial training.

Breachment

Logit Pairing Methods Can Fool Gradient-Based Attacks - NIPS 2018 workshop

Marius Mosbach, Maksym Andriushchenko, Thomas Trost, Matthias Hein, Dietrich Klakow. Logit Pairing Methods Can Fool Gradient-Based Attacks. NIPS 2018 workshop. arXiv:1810.12042