Robust Structure

By LI Haoyang 2020.11.12 (branched)

Content

Robust StructureContentRobust NASWhen NAS Meets Robustness - CVPR 2020One-shot NASRobust architecture search frameworkSearch spaceRobust search algorithm and evaluationRobust architectureArchitecture strategy under budgetTowards a larger search spaceExperimentsInspirations

Robust NAS

When NAS Meets Robustness - CVPR 2020

Code: https://github.com/gmh14/RobNets

Minghao Guo, Yuzhe Yang, Rui Xu, Ziwei Liu, Dahua Lin. When NAS Meets Robustness: In Search of Robust Architectures against Adversarial Attacks. CVPR 2020. arXiv:1911.10695

In this work, we take an architectural perspective and investigate the patterns of network architectures that are resilient to adversarial attacks.

Their search reveals three observations

Densely connected patterns result in improved robustness (Why?)
Under computational budget, adding convolution operations to direct connection edge is effective
Flow of solution procedure (FSP) matrix is a good indicator of network robustness

One-shot NAS

The primary goal of NAS (Network Architecture Search) is to search for computation cells and use them as the basic building unit to construct a whole network. Each cell is a combination of operations chosen from a pre-defined operation space.

The basic process of one-shot NAS is as follows:

Train a supernet containing every possible architectures
Evaluate performances of the subarchitectures taken from the supernet and rank them.
Take out the best-performing architecture and retrain it from scratch.

In this work, they only evaluate the robustness of each subnet rather than take it out and retrain it.

Robust architecture search framework

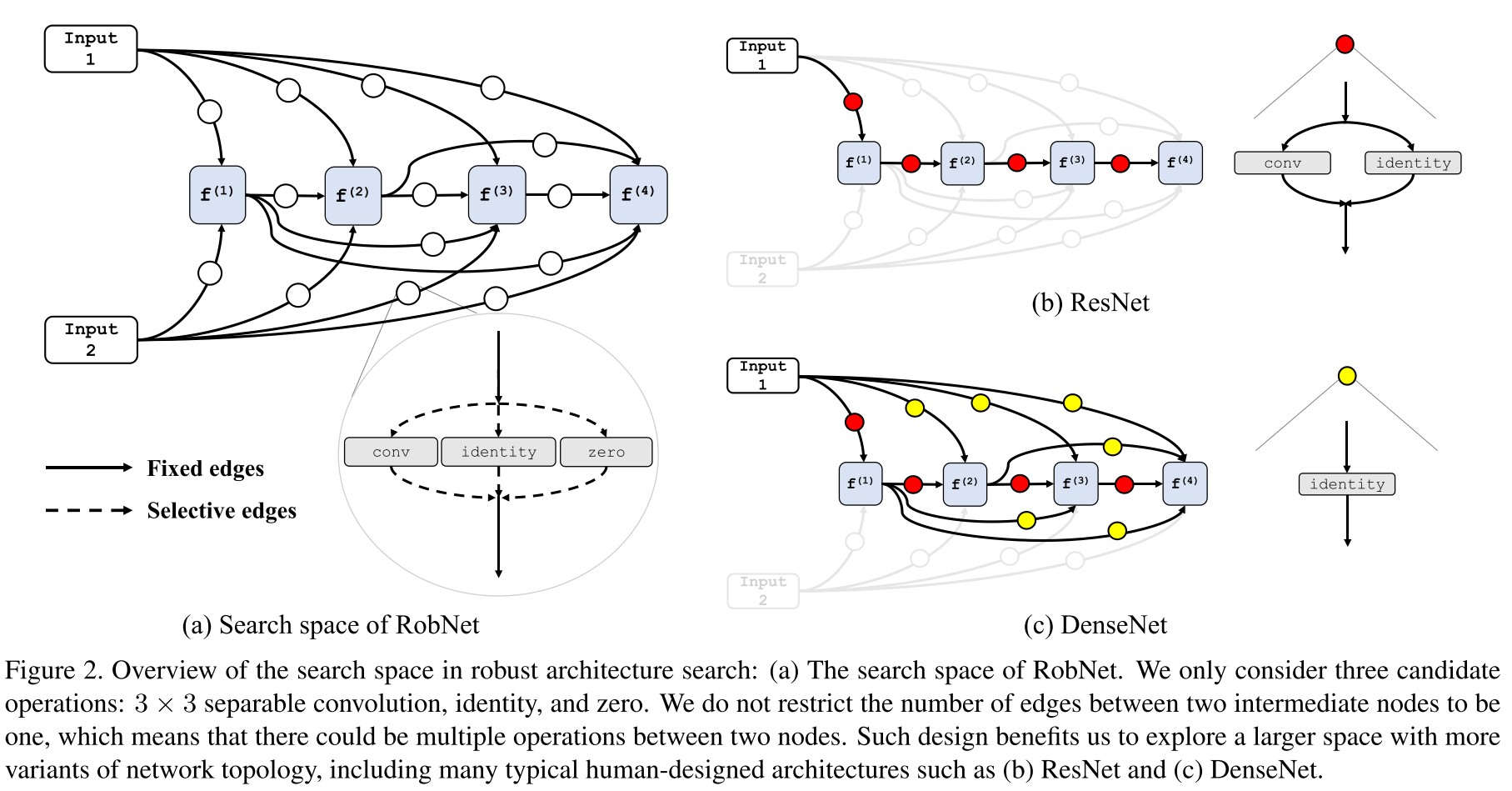
Search space

$G=(V,E)$ $N$ nodes.

$E^{(i,j)}$ $o^{(i,j)}(\cdot)$ $\mathcal{O}=\{o_k(\cdot),k=1,\dots,n\}$ $n$ candidates operations.

$V^{(i)}$ $f^{(i)}$ , computed by

f^{(i)}=\sum_{i<j}o^{(i,j)}(f^{(i)})

The transformation in each edge is computed by

o^{(i,j)}(\cdot)=\sum_{k=1}^{n}\alpha_k^{(i,j)}o_k(\cdot)

$\alpha_k^{(i,j)}$ $k$ th transformation parameters. The architecture is then represented by

\alpha=\{\alpha_k^{(i,j)}|\alpha_k^{(i,j)}\in\{0,1\},i,j=1,\dots,N,k=1,\dots,n\}

direct edge $E^{(i,j)}\in\{E^{(i,j)}|j=i+1\}$ skip edge $E^{(i,j)}\in\{E^{(i,j)}|j>i+1\}$ .

The major differences from conventional NAS are

$3\times 3$ separable convolution, identity and zero.
$o^{(i,j)}(\cdot)$ $n$ operations.

Robust search algorithm and evaluation

For each epoch, they sample a sub-architecture and perform adversarial training on it.

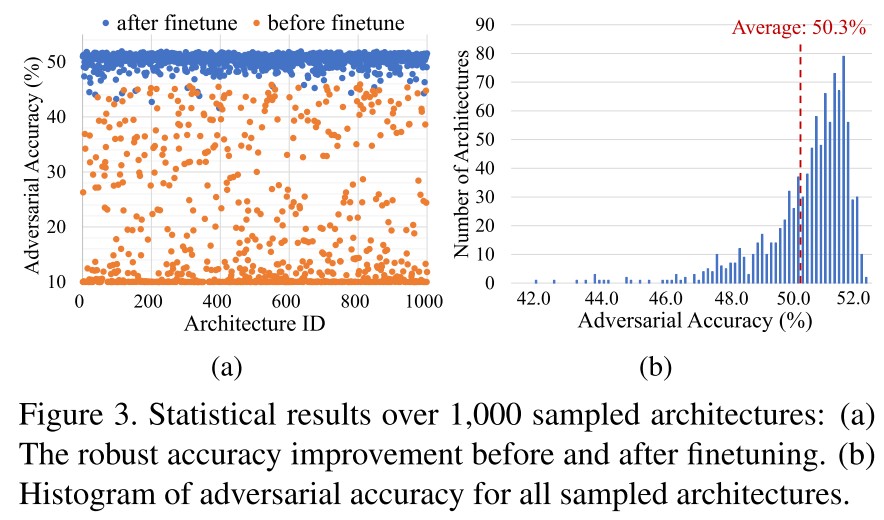
In evaluation, they randomly sample subnets from the supernet and discover that a few epochs' finetuning will increase the robustness very much, the results are shown in Figure 3 (a).

In Figure 3 (b), there is the histogram of adversarial accuracy of 1000 randomly sampled architectures with 3 epochs' finetuning.

Robust architecture

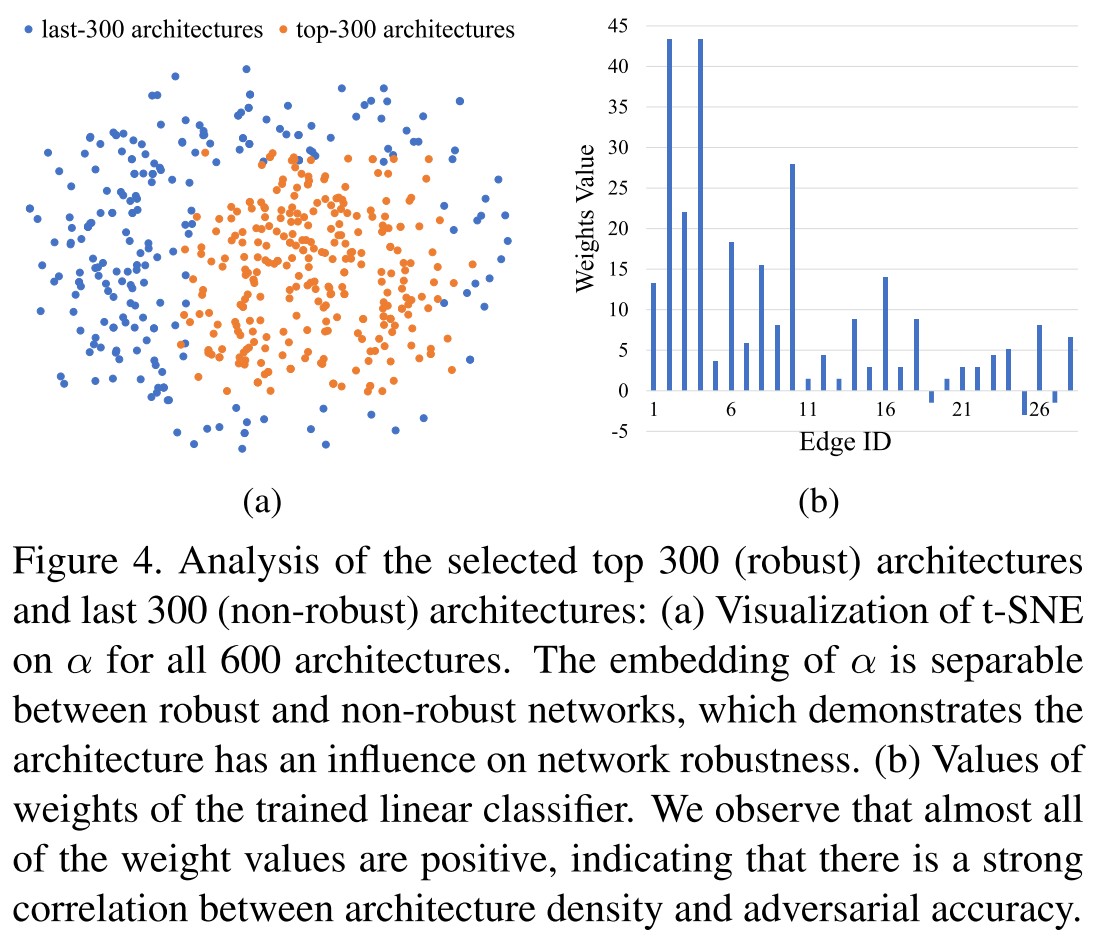
They choose the best 300 and worst 300 architectures in terms of adversarial accuracy and with applied binary labels (robust as 1 and non-robust as -1), using t-SNE on the parameters, there shows in Figure 4(a) that these architectures are separable.

They then train a simple linear classifier to classify these two classes of architectures and visualize the weights of the classifier finding that almost all of the weight values are positive as shown in Figure 4 (b).

They think it indicates there is a strong correlation between architecture density and adversarial accuracy (why?).

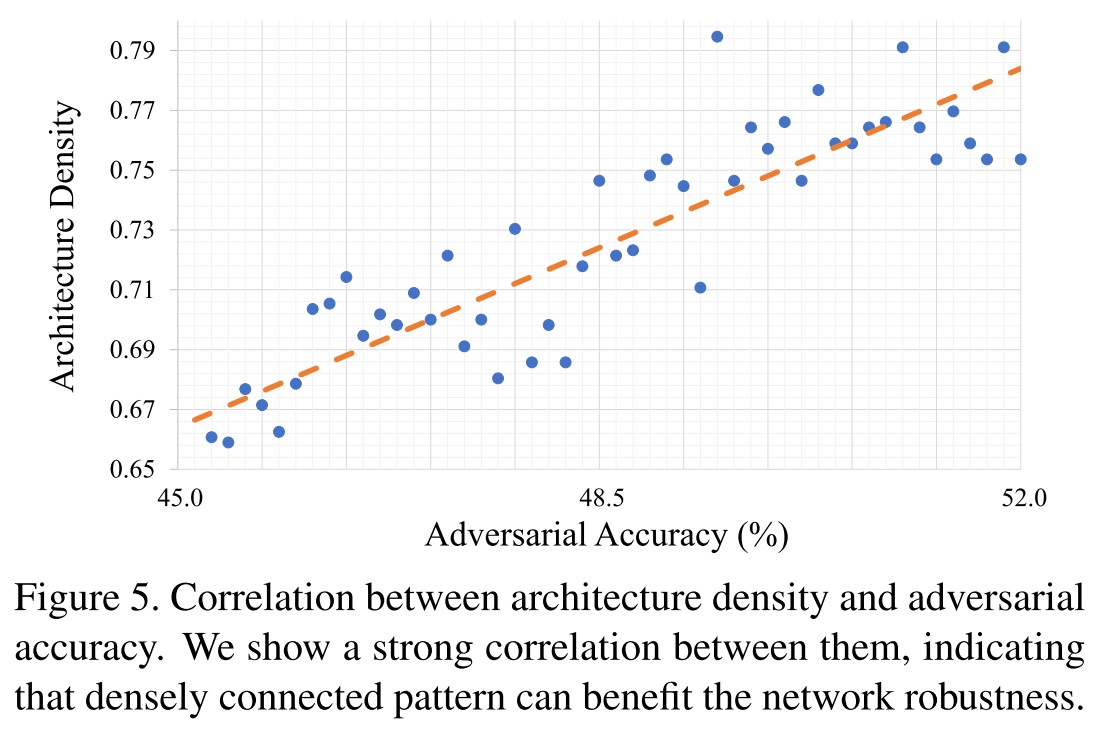
They define the architecture density as the number of connected edges over the total number of all possible edges, i.e.

D=\frac{|E_{connected}|}{|E|}=\frac{\sum_{i,j,k}\alpha_k^{(i,j)}}{|E|}

As shown in Figure 5, they verify and conclude that densely connected pattern can benefit the network robustness.

This is an interesting observation, but requires more explanation.

Architecture strategy under budget

If we are given a fixed total number of parameters (or we refer to as a computational budget), how to obtain architectures that are more robust under the limited constraint?

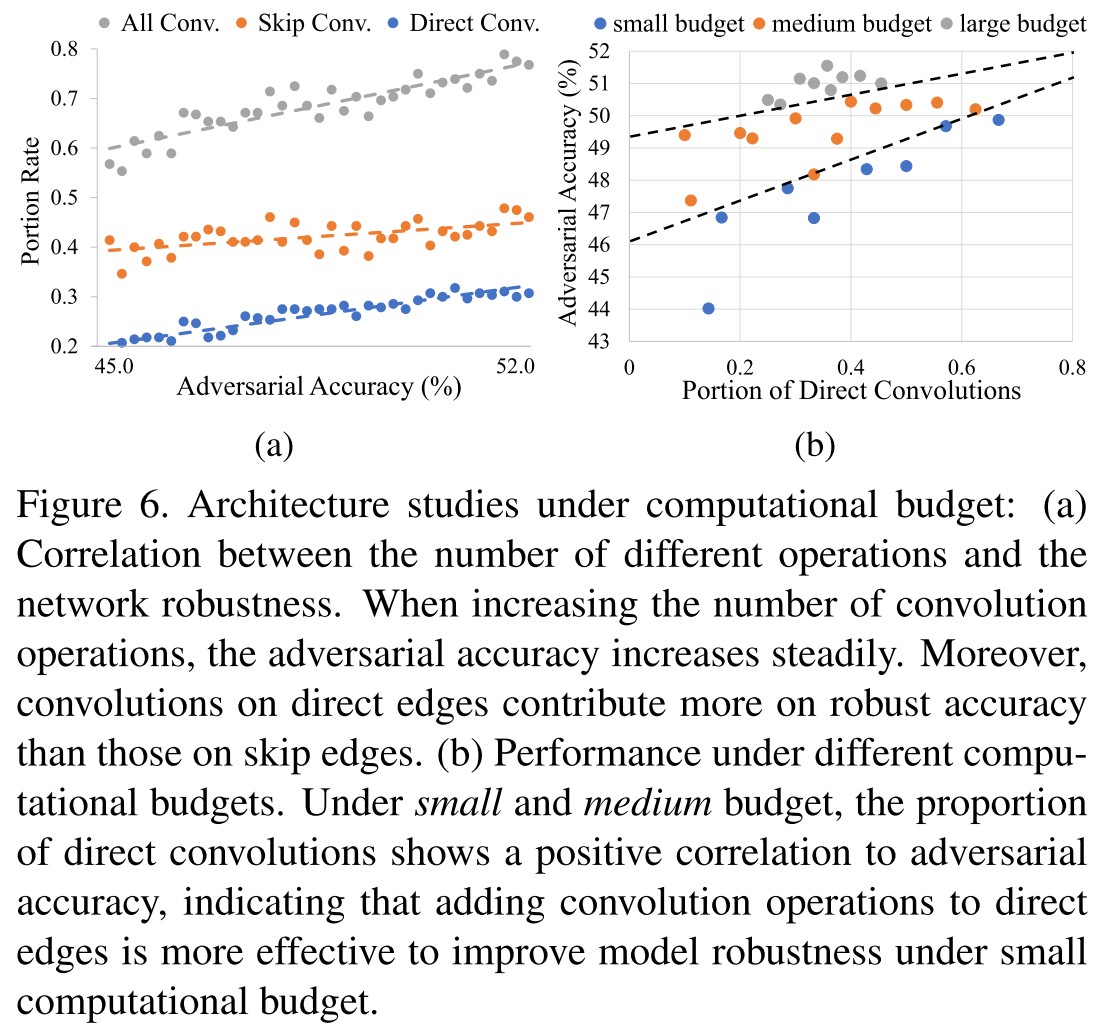
In Figure 6 (a), they depicted the effect of the number of convolution operations and as shown

With the number of convolution operations increases, the adversarial accuracy improves steadily.

The results declare that convolutions on direct edges contribute more on adversarial accuracy than those on skip edges.

In Figure 6 (b), they evaluate the architectures under budget of small, medium and large.

For each of the budget, we randomly sample 100 architectures, evaluate their adversarial accuracy following Sec. 3.2 and calculate the proportion of convolutions on direct edges among all convolutions.

For small and medium budget, the proportion of direct convolutions has a positive correlation to adversarial accuracy.

They conclude that

Under small computational budget, adding convolution operations to direct edges is more effective to improve model robustness

Towards a larger search space

In this section, we relax the cell-based constraint and conduct studies on a larger architecture search space.

To handle the exploded searching space, they propose a Feature Flow Guided Search.

$l$ th layer, the FSP is

G_{l}(x;\theta)=\sum_{s=1}^h\sum_{t=1}^w\frac{F_{l,s,t}^{in}(x;\theta)\times F_{l,s,t}^{out}(x;\theta)}{h\times w}

$F_{l}^{in}(x;\theta)$ $F_{l}^{out}(x;\theta)$ denotes the output feature map.

For a given network, the distance of FSP matrix between adversarial example and clean data for each cell of the network can be calculated as

L_{l}^{FSP}=\frac{1}{N}\sum_{x}||G_{l}(x;\theta)-G_{l}(x^{'};\theta)||_2^2

We sample 50 architectures without finetuning for the cell-free search space and evaluate the gap of clean accuracy and adversarial accuracy for each architecture.

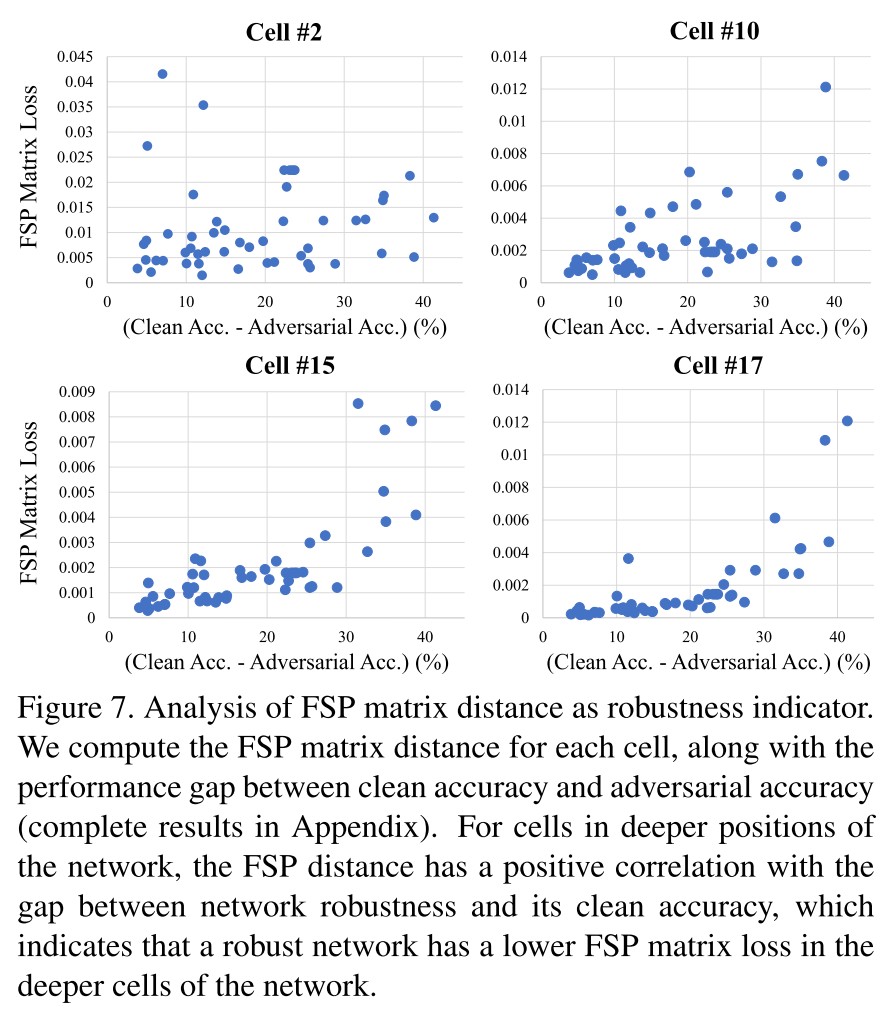
We also calculate the FSP matrix distance for each cell of the network and show representative results in Fig. 7

Based on the observations from Figure 7, they conclude that

A robust network has a lower FSP matrix loss in the deeper cells of network.

It's actually expected, given the observation in Feature Denoising that the adversarial example tends to activate a much more noisy feature map, therefore, in the deeper cells, a more robust model should be able to draw the feature maps of clean and adversarial examples together.

Experiments

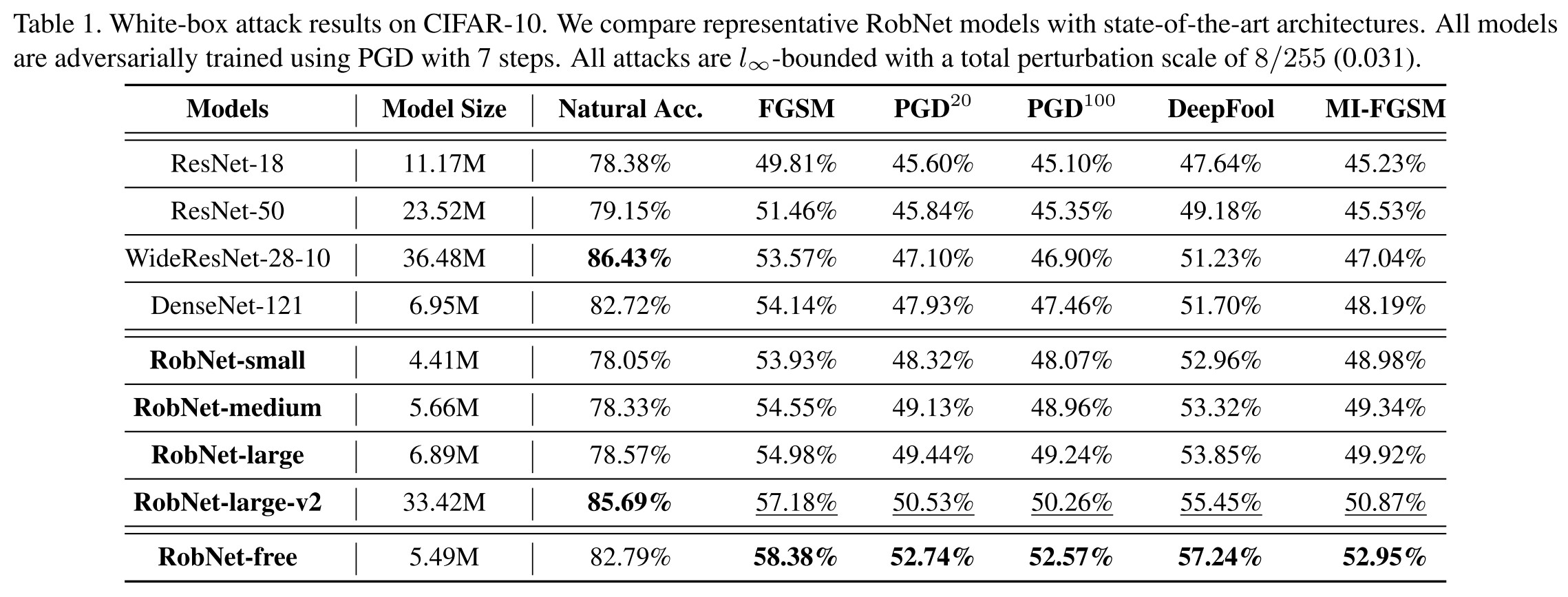
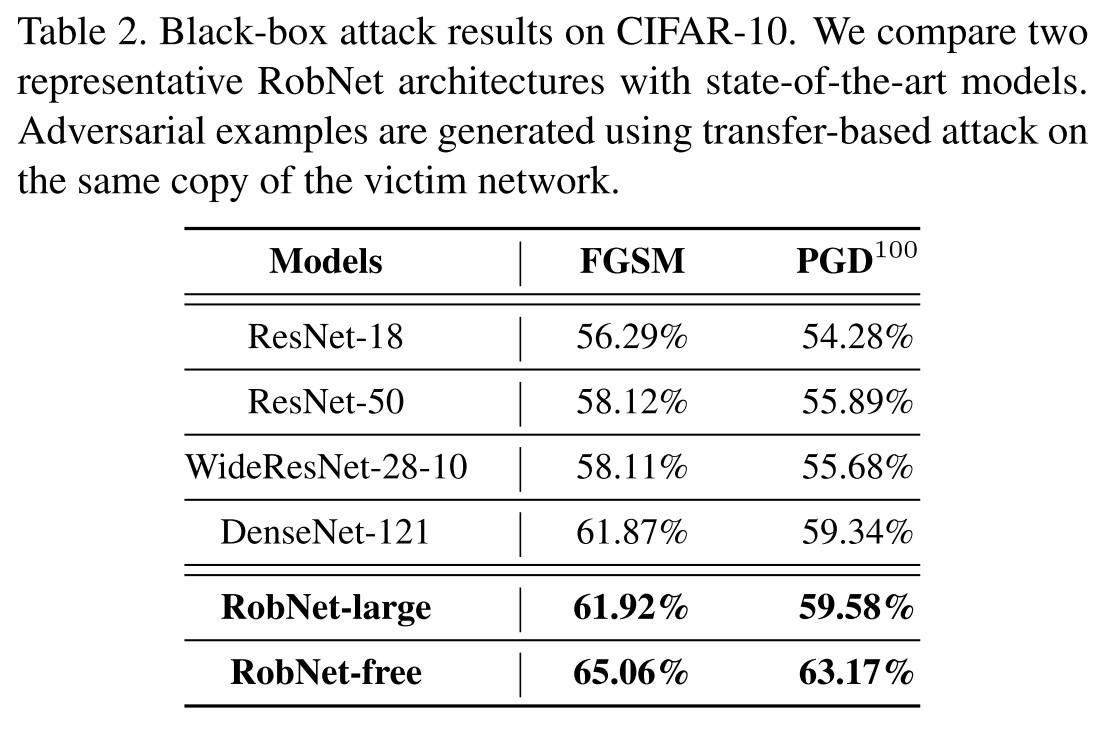
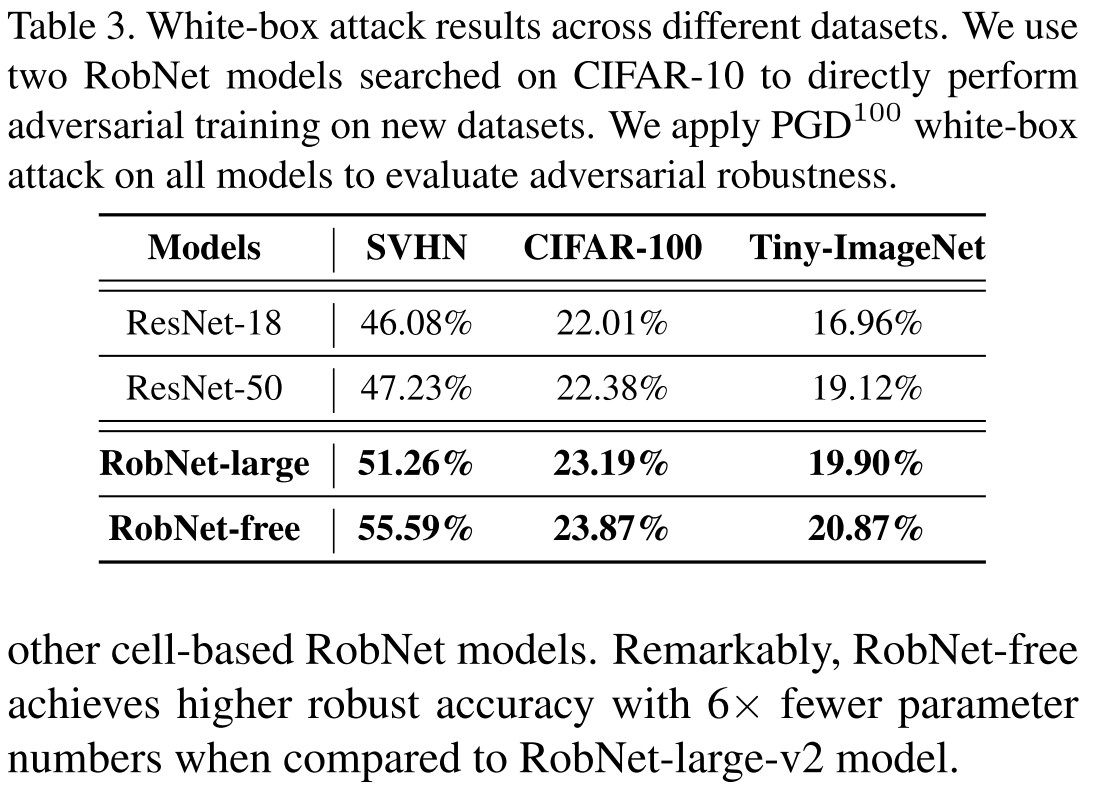
Three selected architectures from supernet are labeled RobNet-small, RobNet-medium and RobNet-large.

RobNet-free is a representative architecture among those found by FSP guided search.

Inspirations

This is the first paper combining NAS and adversarial training, which is an interesting topic. They make three observations. The last one is quite expected based on the previous work.

The first and the second observation all involves the density of connections in the network architecture. I think there is a possibility that the conclusion in the second observation, i.e. that direct edges are better than skip edges in networks with smaller parameters in terms of adversarial accuracy may because of the dropping of network density brought by skip edges, so these two observations become one.

There remains a question to answer now:

Why a denser network performs better?

Intuitively, I think a denser network makes the generation of adversarial examples more complicated (indicating gradient masking), but they actually combine it with adversarial training, excluding the problem of gradient masking.