Restricted Adversarial Attacks

By LI Haoyang 2020.11.30

Content

Robust Attack

Synthesizing Robust Adversarial Examples - ICML 2018

Anish Athalye, Logan Engstrom, Andrew Ilyas, Kevin Kwok. Synthesizing Robust Adversarial Examples. ICML 2018. arXiv:1707.07397

This is the source of Expectation OverTransformation, the base for many applicable adversarial attacks.

Prior work has shown that adversarial examples generated using these standard techniques often lose their adversarial nature once subjected to minor transformations (Luo et al., 2016; Lu et al., 2017).

Expectation Over Transformation

$Y$ $X$ $P(y|x)$ $\nabla_xP(y|x)$ $y\in Y$ $x\in X$ .

$y_t$ $\epsilon$ -radius ball, the adversarial examples are generated by maximizing the log-likelihood, i.e.

\arg\max_{x^\prime}\log P(y_t|x^\prime)\\ \text{subject to }||x^\prime-x||_p<\epsilon,x^\prime\in[0,1]^d

However, prior work has shown that these adversarial examples fail to remain adversarial under image transformations that occur in the real world, such as angle and viewpoint changes (Luo et al., 2016; Lu et al., 2017).

To deal with this problem, they incorporate potential transformations into the generating process and propose Expectation Over Transformation (EOT).

$T$ $t$ $x^\prime$ $t(x^\prime)$ $d(\cdot,\cdot)$ , EOT aims to constrain the expected effective distance between the adversarial and original inputs, i.e.

\delta=\Bbb{E}_{t\sim T}[d(t(x^\prime),t(x))]

and the corresponding optimization becomes:

\arg\max_{x^\prime}\Bbb{E}_{t\sim T}[\log P(y_t|t(x^\prime))]\\ \text{subject to }\Bbb{E}_{t\sim T}[d(t(x^\prime), t(x))]<\epsilon, x\in[0,1]^d

$T$ can model perceptual distortions such as random rotation, translation, or addition of noise.

A direct and simple idea.

$T$ , distance metric, and optimization method.

2D case
$t(x)=Ax+b$ .
3D case
$x$ $t(x)$ $x$ applied.
$x$ $Mx + b$ $M$ $b$ .

Optimization Objective

They take the form proposed by Carlini & Wagner, i.e.

\arg\max_{x^\prime}\left(\Bbb{E}_{t\sim T}[\log P(y_t|t(x^\prime))]-\lambda\Bbb{E}_{t\sim T}[d(t(x^\prime), t(x))]\right)

$d(x^\prime, x)$ $\ell_2$ norm in the LAB color space where Euclidean distance roughly corresponds with perceptual distance.

The final objective then becomes:

\arg\max_{x^\prime}\Bbb{E}_{t\sim T}[\log P(y_t|t(x^\prime))-\lambda||LAB(t(x^\prime))-LAB(t(x))||_2]

We use projected gradient descent to maximize the objective, and clip to the set of valid inputs (e.g. [0, 1] for images).

Evaluation

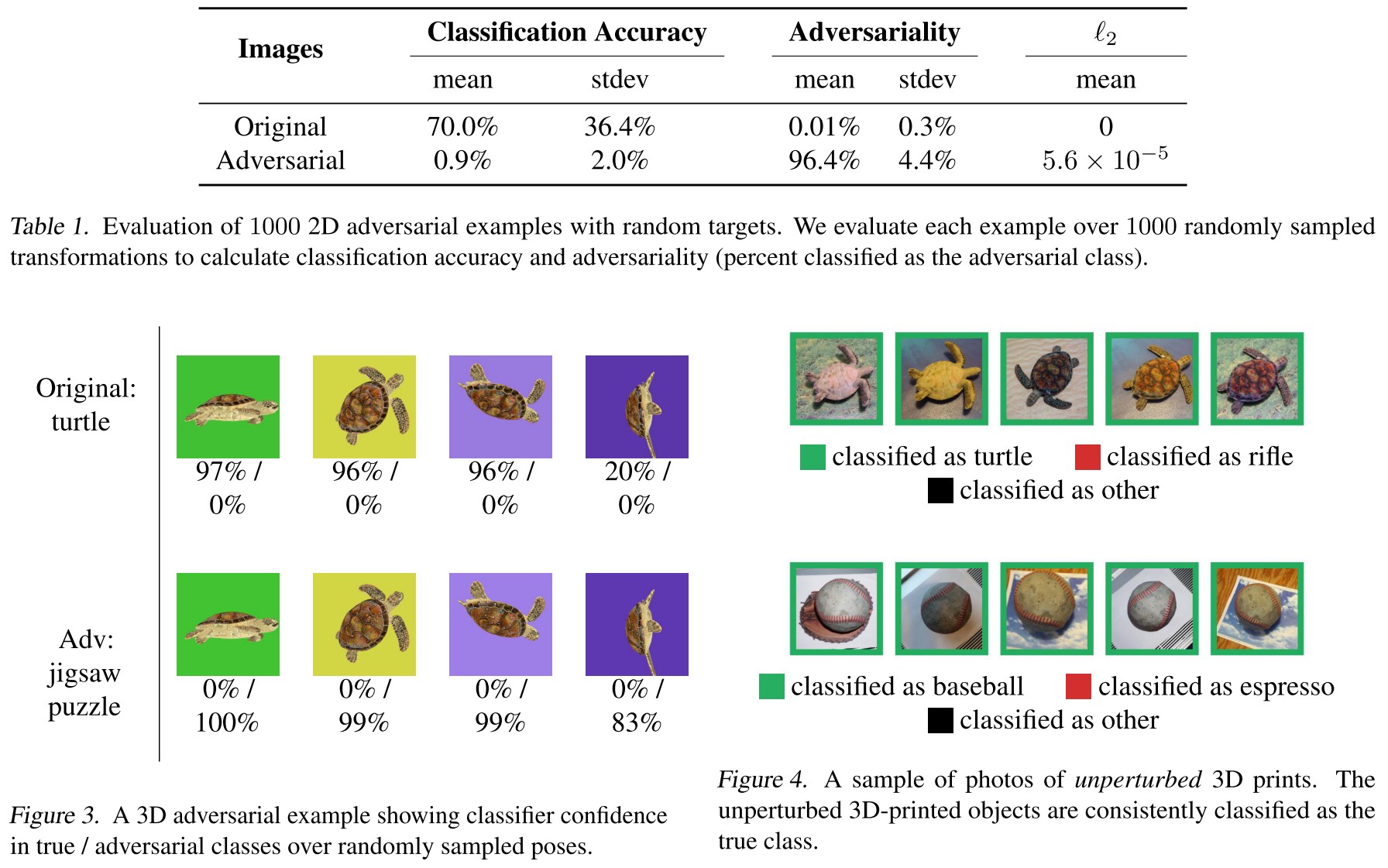
The adversariality is measured by

\Bbb{E}_{t\sim T}[C(t(x^\prime),y_{adv})]\\ C(x,y)=\begin{cases} 1&\text{if }x\text{ is classified as } y\\ 0&\text{otherwise} \end{cases}

$y_{adv}$ is a target class different from original classes.

Many results are omitted.

Spatial Restricted

One pixel attack for fooling deep neural networks - CVPR 2017

Jiawei Su, Danilo Vasconcellos Vargas, Sakurai Kouichi. One pixel attack for fooling deep neural networks. CVPR 2017. arXiv:1710.08864

In this paper, by perturbing only one pixel with differential evolution, we propose a black-box DNN attack in a scenario where the only information available is the probability labels (Figure 1 and 2).

They managed to use Differential Evolution to craft one-pixel attack, which is surprising but not very inspiring, therefore it's better to just check the results.

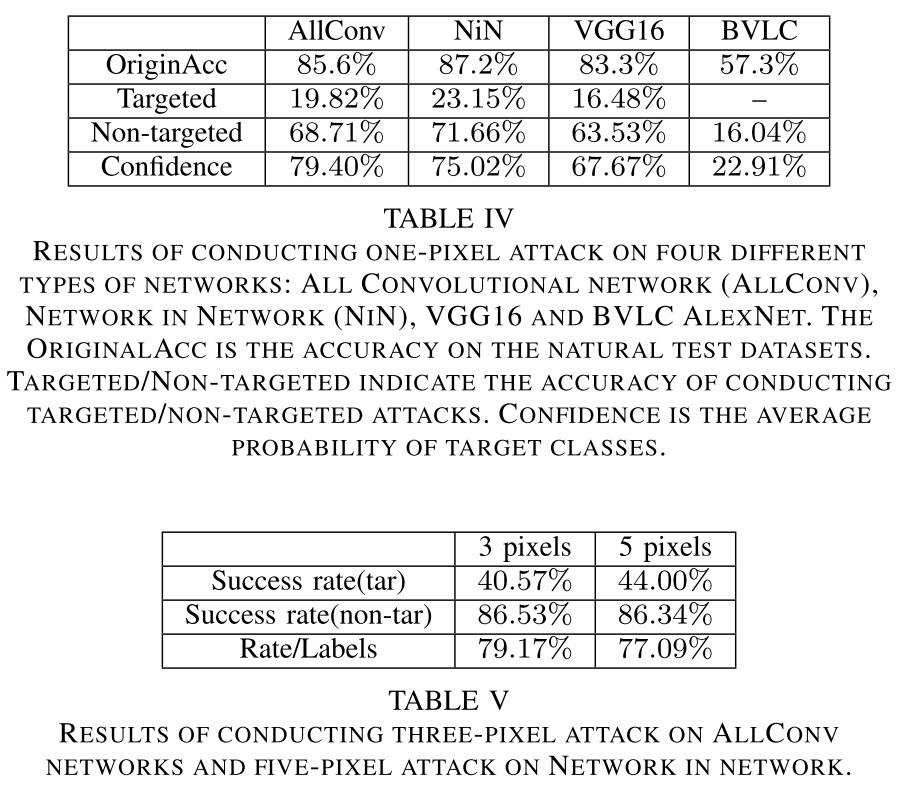
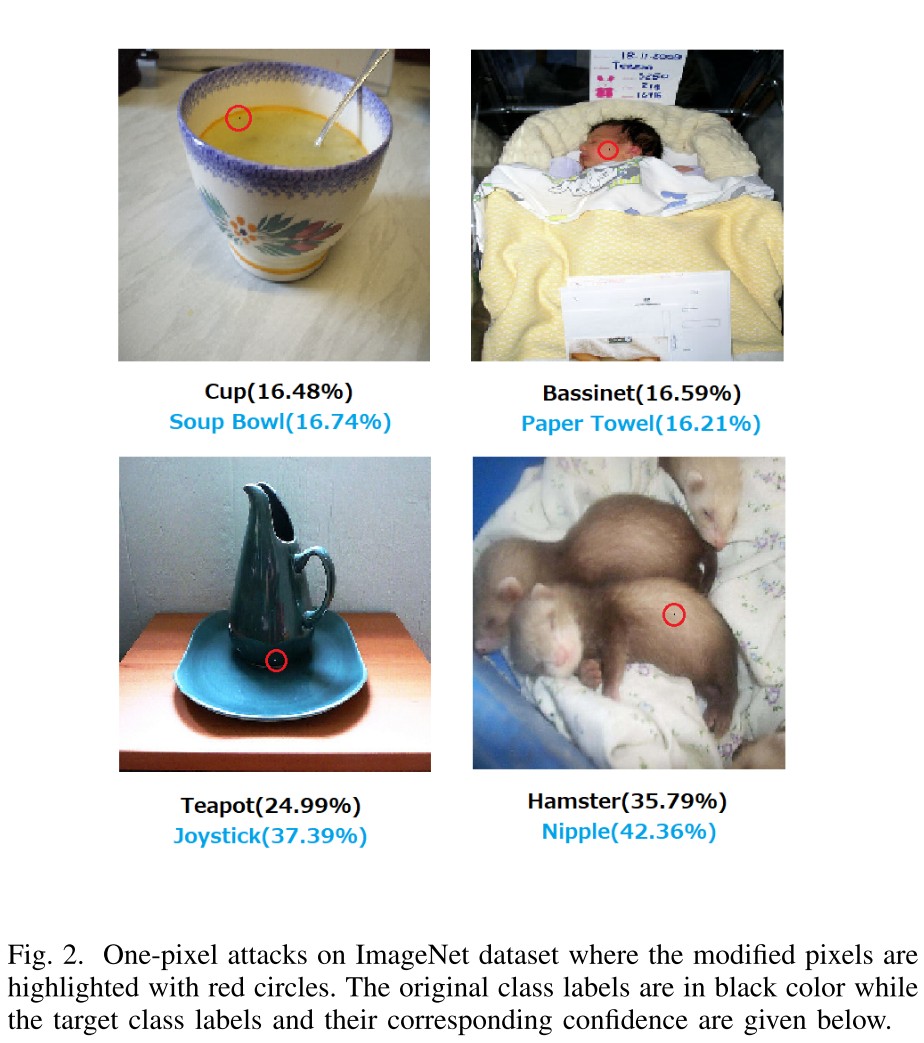
Spectral Restricted

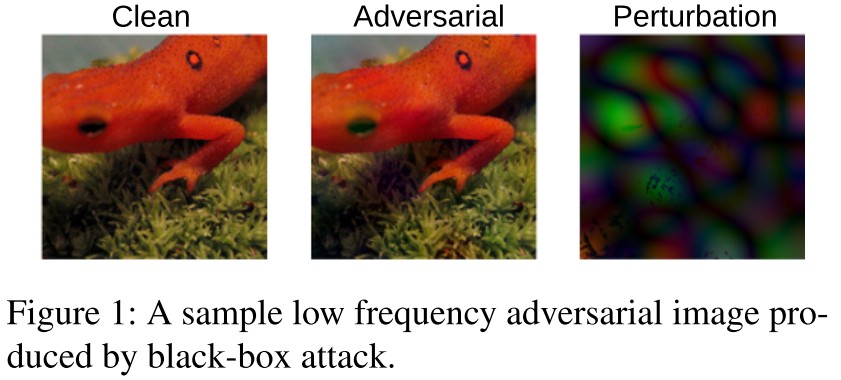
Low Frequency Adversarial Perturbation - UAI 2019

Chuan Guo, Jared S. Frank, Kilian Q. Weinberger. Low Frequency Adversarial Perturbation. UAI 2019. arXiv:1809.08758

In the black-box setting, the absence of gradient information often renders this search problem costly in terms of query complexity.

In this paper we propose to restrict the search for adversarial images to a low frequency domain.

They propose to search adversarial examples in the black-box settings in low frequency domain, and prove that it accelerate the searching by 2 to 4 times.

Low frequency subspace

The inherent query inefficiency of gradient estimation and decision-based attacks stems from the need to search over or randomly sample from the high-dimensional image space.

Thus the query complexity depends on the relative adversarial subspace dimensionality compared to the full image space, and finding a low-dimensional subspace that contains a high density of adversarial examples can improve these methods.

Most of the content-defining information in natural images live in the low end of the frequency spectrum as utilized by JPEG.

It is therefore plausible to assume that CNNs are trained to respond especially to low-frequency patterns in order to extract class-specific signatures from images.

Motivated by it, they propose to restrict the search space to the low-frequency spectrum.

Discrete cosine transform (DCT)

$X\in\R^{d\times d}$ , define basis functions

\phi_d(i,j)=\cos\left[\frac{\pi}{d}(i+\frac{1}{2})j\right],1\le i,j\le d

$V=DCT(X)$ is defined as

V_{j_1,j_2}=N_{j_1}N_{j_2}\sum_{i_1=0}^{d-1}\sum_{i_2=0}^{d-1}X_{i_1,i_2}\phi_d(i_1,j_1)\phi_d(i_2,j_2),N_j=\begin{cases} \sqrt{\frac{1}{d}}&j=0\\ \sqrt{\frac{2}{d}}&otherwise \end{cases}

$N_{j_1},N_{j_2}$ $||X||_2=||DCT(X)||_2$ .

$V_{i,j}$ $\phi_d(i,j)$ $i,j$ .

$X=IDCT(V)$ is

X_{i_1,i_2}=\sum_{j_1=0}^{d-1}\sum_{j_2=0}^{d-1}N_{j_1}N_{j_2}V_{j_1,j_2}\phi_d(i_1,j_1)\phi_d(i_2,j_2)

Both DCT and IDCT are applied channel-wise independently for images with multiple channels.

Sampling low frequency noise

$\mathcal{D}$ $\R^{d\times d}$ $\tilde{\eta}\in\R^{d\times d}$ in frequency space so that

\tilde{\eta}_{i,j}=\begin{cases} x_{i,j}\sim\mathcal{D}&\text{if }1\le i,j\le rd\\ 0&\text{otherwise} \end{cases}

$r$ is a factor parameter controlling the low frequency size.

The corresponding noise "image" in pixel space is then defined by

\eta=IDCT(\tilde{\eta})

$\eta$ $rd$ .

$IDCT_r(\mathcal{D})$ .

Low frequency noise success rate

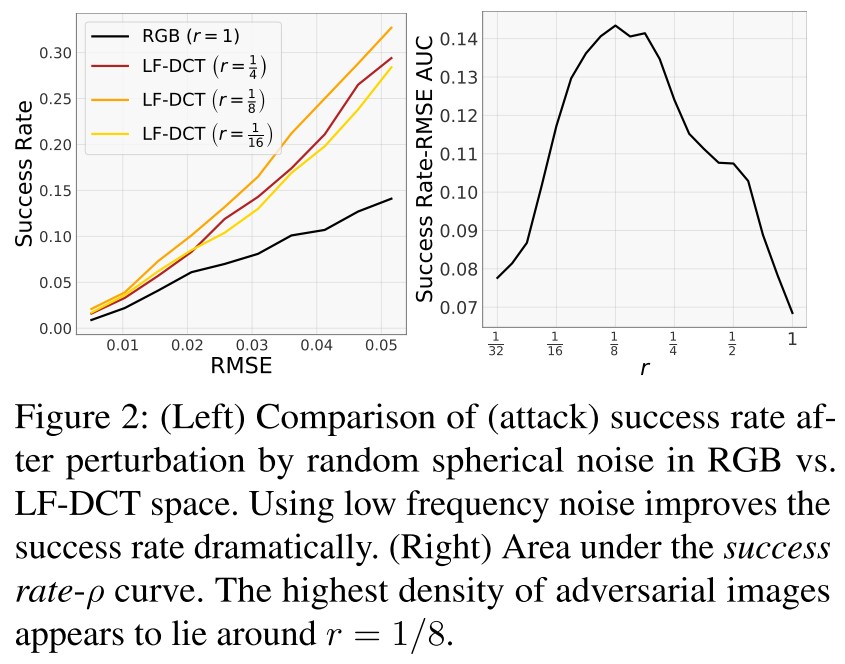
They compute the success rate in RGB and LF-DCT space of random noises on ResNet-50 trained for ImageNet.

We sample the noise vector η uniformly from the surface of the unit sphere of radius ρ > 0 in the rd × rd LF-DCT space and project it back to RGB through the IDCT transform.

Here they conclude:

$\rho$ $r$ .
$r = 1/8$ $1/64$ .
$r = 1$ , which corresponds to no dimensionality reduction (and is identical to sampling in the original RGB space)

This is further verified in Hold me Tight !, where the adversarially trained models also seem to be more sensitive to low frequency changes.

Low frequency gradient descent

$\ell_p$ denote the adversarial loss, e.g. the C&W loss

\ell_y(\bold{x}^\prime)=\max\left(Z(\bold{x}^\prime)_y-\max_{y^\prime\neq y}Z(\bold{x}^\prime)_{y^\prime}+\kappa,0\right)

$r\in[0,1]$ $v\in\R^{rd\times rd}$ $V\in\R^{d\times d}$ by

V_{i,j}=\begin{cases} v_{i,j}&\text{if }1\le i,j\le rd\\ 0&\text{otherwise} \end{cases}

The low-frequency perturbation domain is then parametrized as

\Delta=IDCT(V)

$\Delta$ $V$ $\overline{\Delta}$ $\overline{V}$ , i.e.

\overline{\Delta}_{i_1*d+i_2}=\Delta_{i_1,i_2}\\ \overline{V}_{i_1*d+i_2}=V_{i_1,i_2}

It's the commonly used np.reshape(-1).

$\overline{\Delta}$ $\overline{V}$ .

$\bold{z}$ , its right-product with the Jacobian of IDCT is given by

J_{IDCT}\cdot \bold{z}=DCT(\bold{z})

Thus it's possible to apply the chain rule to compute

\frac{\partial \ell}{\partial V}=DCT(\frac{\partial\ell}{\partial\Delta}),\frac{\partial\ell}{\partial v}=[\frac{\partial \ell}{\partial V}]_{1:rd,1:rd}

$V=DCT(\Delta)$ .

which is equivalent to applying DCT to the gradient and dropping the high frequency coefficients.

It makes the implementation relatively simple, and it seems to indicate that high frequency gradient is also some noise for adversarial attack.....

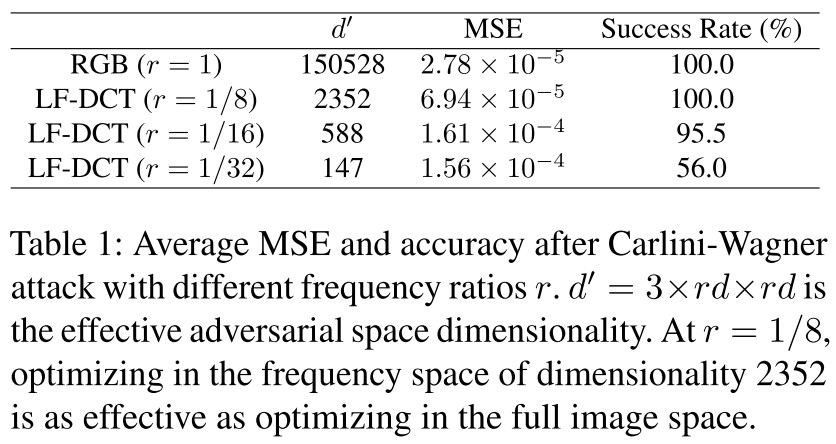
As shown in Figure 3 and Table 1, the low-frequency attack increases the MSE by 3 times, but still imperceptible to human eyes, and the generated adversarial pattern is relatively smooth.

Sharma, Ding, and Brubaker [2019] showed that low frequency gradient-based attacks enjoy greater efficiency and can transfer significantly better to defended models.

Furthermore, they observe that the benefit of low frequency perturbation is not merely due to dimensionality reduction — perturbing exclusively the high frequency components does not give the same benefit.

Application to black-box attacks

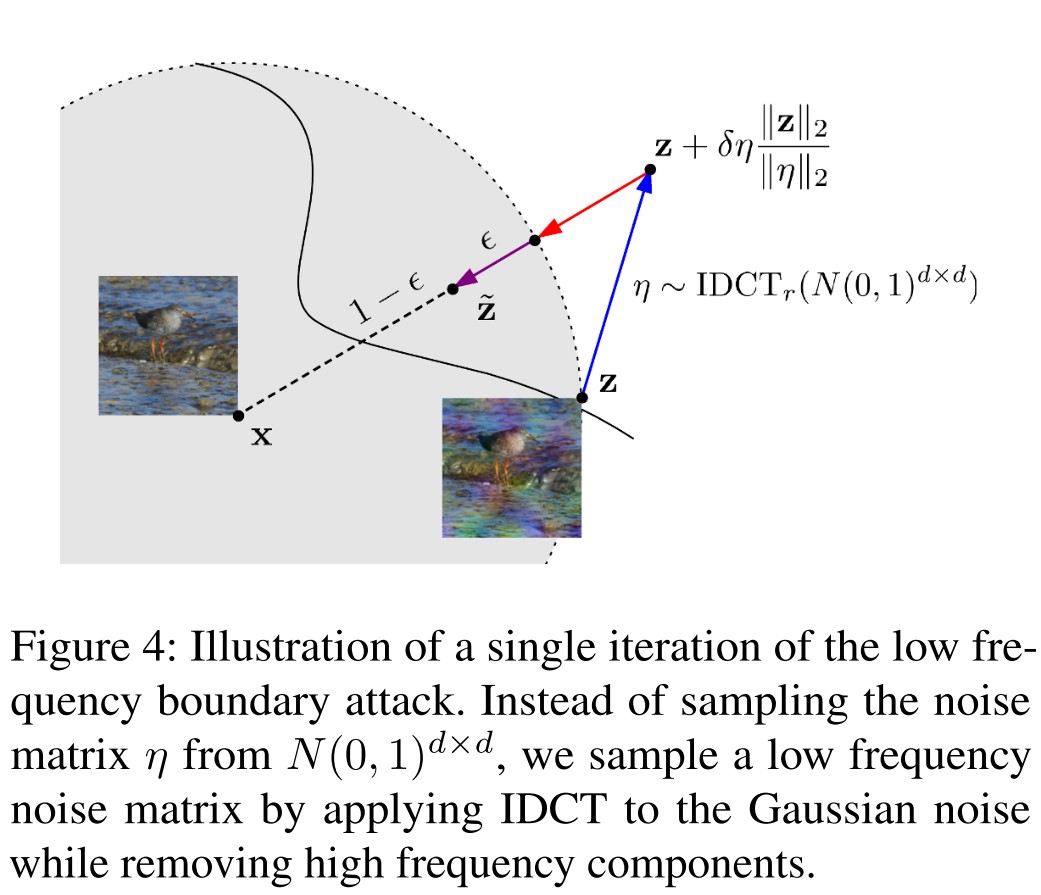
Boundary attack

Proposed in

Brendel, W.; Rauber, J.; and Bethge, M. 2017. Decision-based adversarial attacks: Reliable attacks against black-box machine learning models. CoRR abs/1712.04248

This attack works as follows:

$\eta\sim N(0,1)^{d\times d}$ .
$\bold{z}$ after appropriate scaling.
$\bold{x}$ .
$\bold{z}$ $\bold{x}$ $\tilde{\bold{z}}$ .
Iterate from 1 to 4.

It works like a gradient-free reverse projected gradient descent attack.

low frequency boundary attack (LF-BA) $IDCT_r(N(0,1)^{d\times d})$ .

NES attack

Natural evolution strategies (NES) is a black-box optimization proposed in

Wierstra, D.; Schaul, T.; Glasmachers, T.; Sun, Y.; Peters, J.; and Schmidhuber, J. 2014. Natural evolution strategies. Journal ofMachine Learning Research 15(1):949–980

and it's used for black-box adversarial attack in

Ilyas, A.; Engstrom, L.; Athalye, A.; and Lin, J. 2018. Black-box adversarial attacks with limited queries and information. In Proceedings ofthe 35th International Conference on Machine Learning, ICML 2018, Stockholmsmässan, Stockholm, Sweden, July 10-15, 2018, 2142–2151

$\bold{z}$ $\mathcal{D}$ and minimize:

\min_{\bold{z}}\Bbb{E}_{\eta\sim\mathcal{D}}[\ell(\bold{z}+\eta)]\ \ s.t. d(\bold{x},\bold{z})\le\rho

where:

$\rho$ is some perceptibility threshold
$\mathcal{D}$ $N(0,\sigma^2)^{d\times d}$

The gradient is then

\nabla_{\bold{z}}\Bbb{E}_{\eta\sim\mathcal{D}}[\ell(\bold{z}+\eta)]=\frac{1}{\sigma^2}\Bbb{E}_{\eta\sim\mathcal{D}}[\ell(\bold{z}+\eta)\cdot\eta]

$\eta_1,\dots,\eta_m\sim N(0,\sigma^2)^{d\times d}$ and computing the stochastic gradient

\nabla_{\bold{z}}\Bbb{E}_{\eta\sim\mathcal{D}}[\ell(\bold{z}+\eta)]\approx\frac{1}{m\sigma^2}\sum_{i=1}^m\ell(\bold{z}+\eta_i)\cdot\eta_i

$z$ away from regions of low adversarial density.

Their modified version, named as low frequency NES (LF-NES), constrains the noises to be sampled from a low-frequency subspace.

Experiments

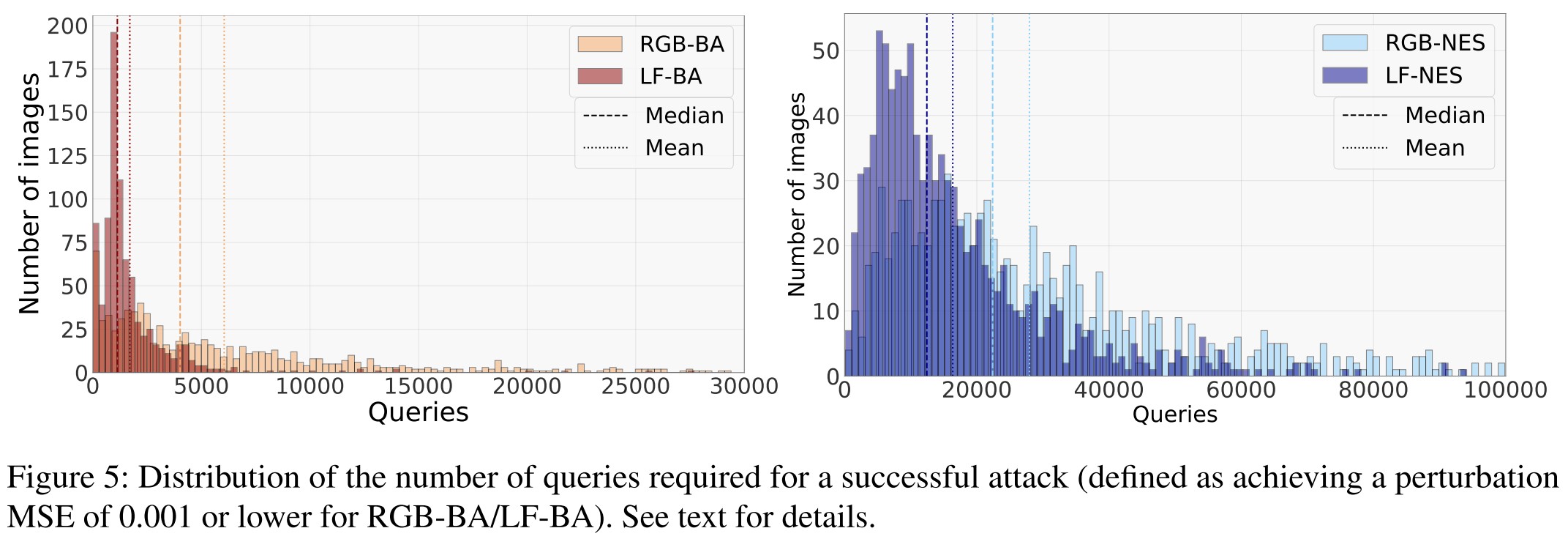
As shown in Figure 5,

The histograms of LF-BA (dark red) and LF-NES (dark blue) are shifted left compared to their Gaussian-based counterparts.

Using low-frequency perturbations reduces the queries required by either of these two black-box attacks.

And it also reveals to be able to breach transformation based defenses.

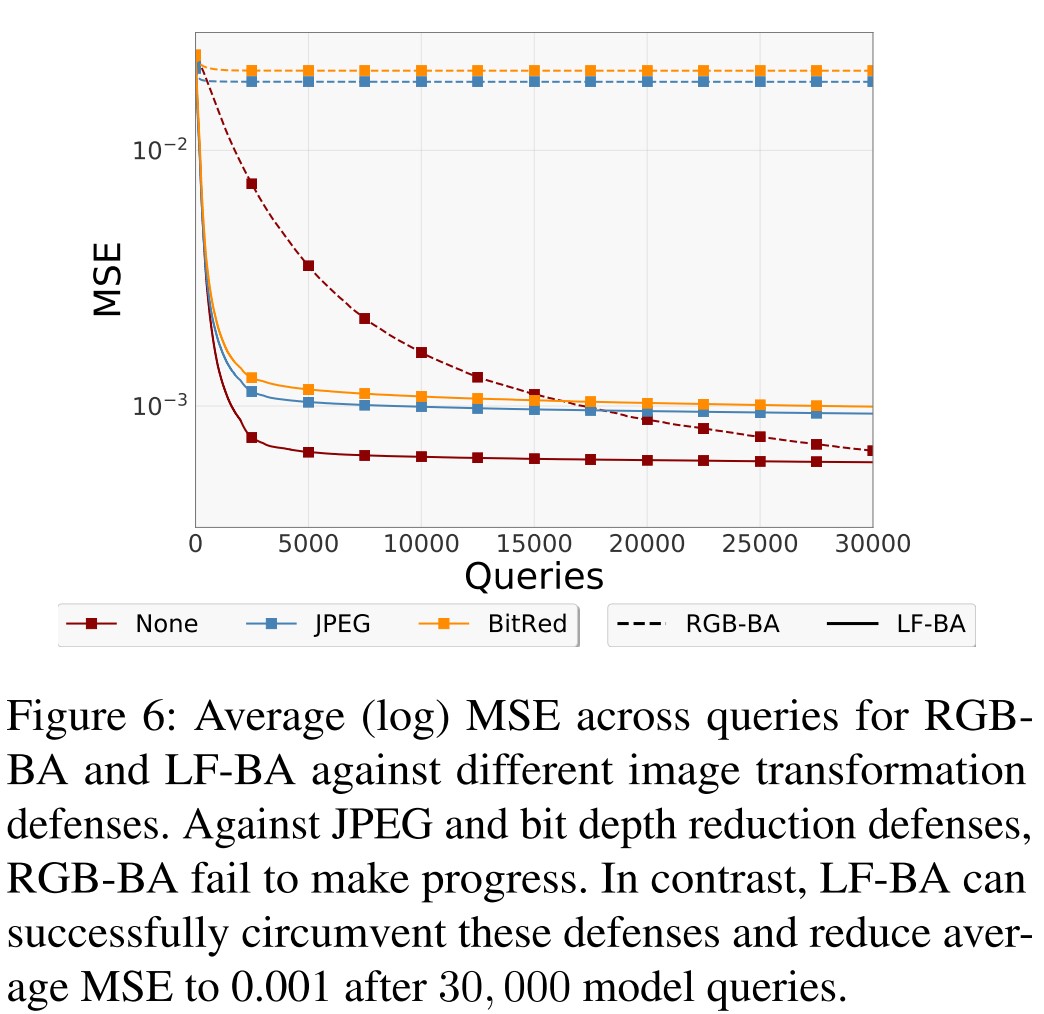
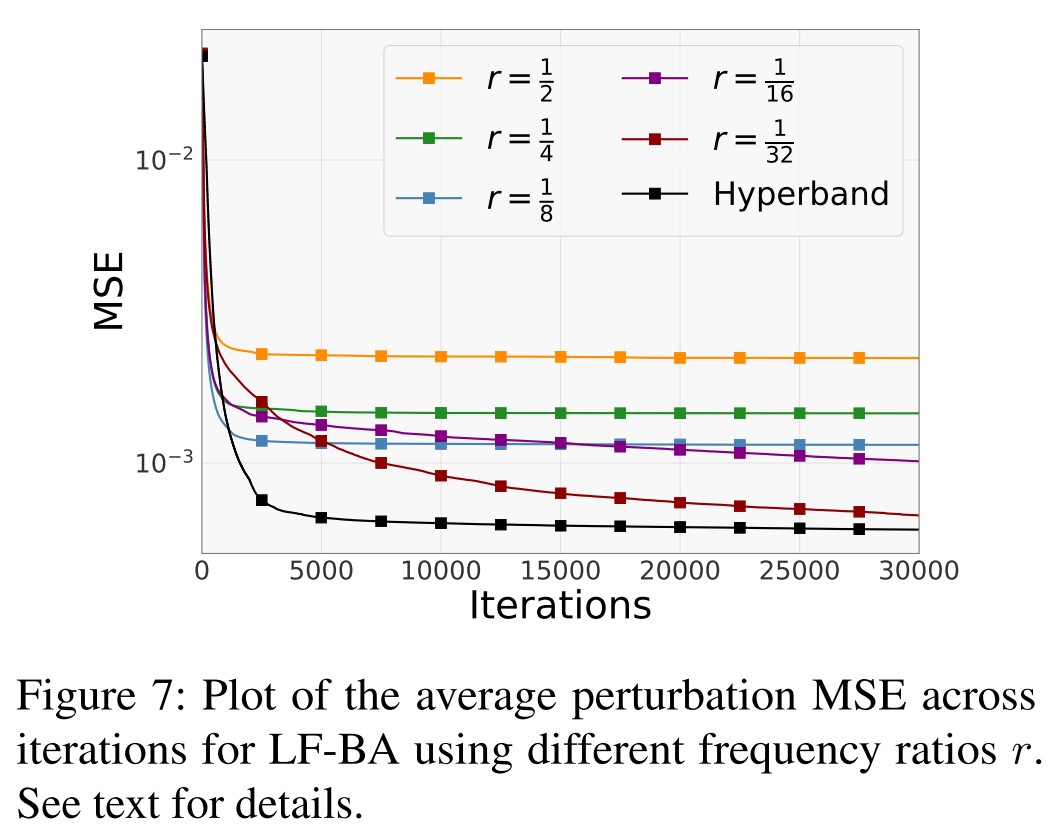
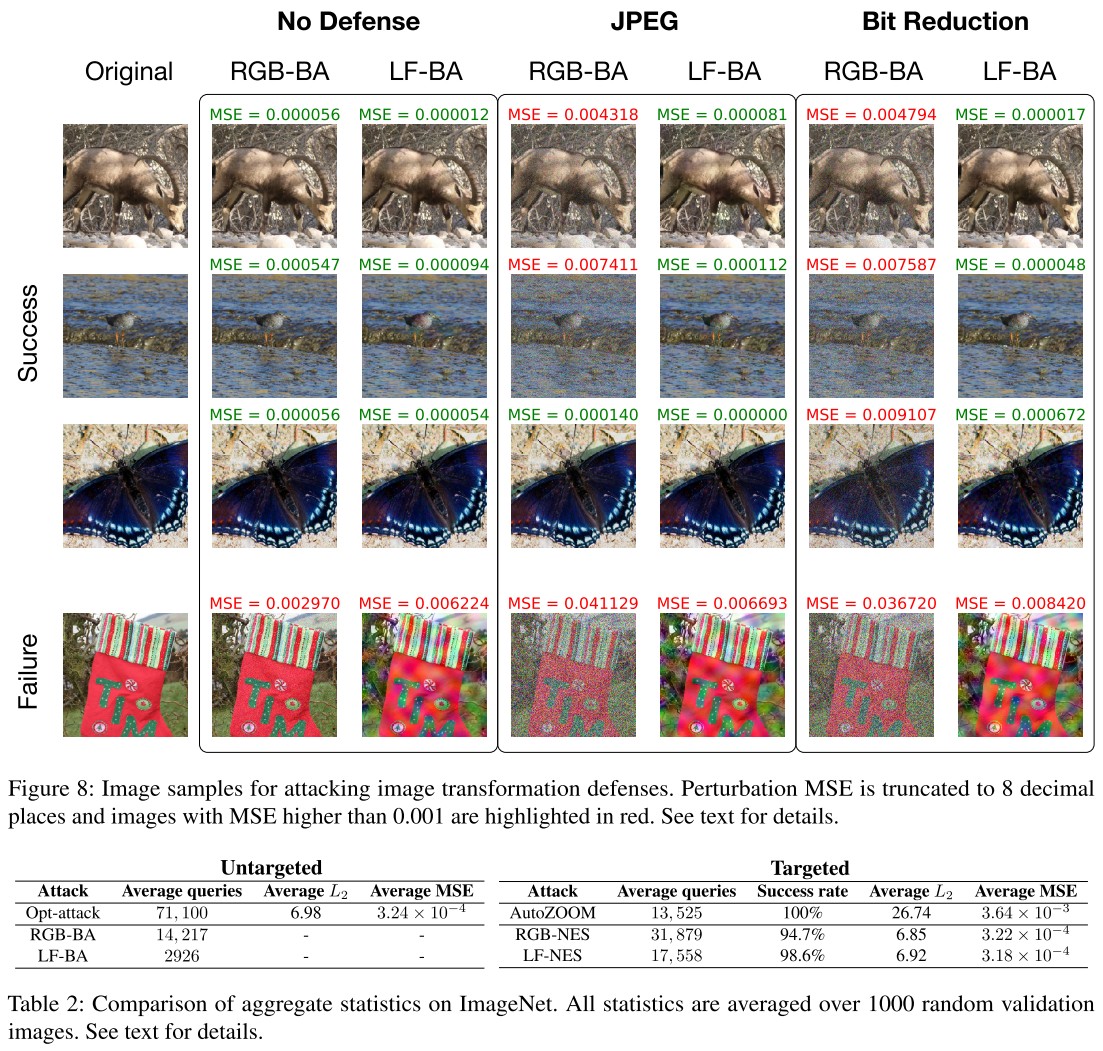
and the google vision cloud

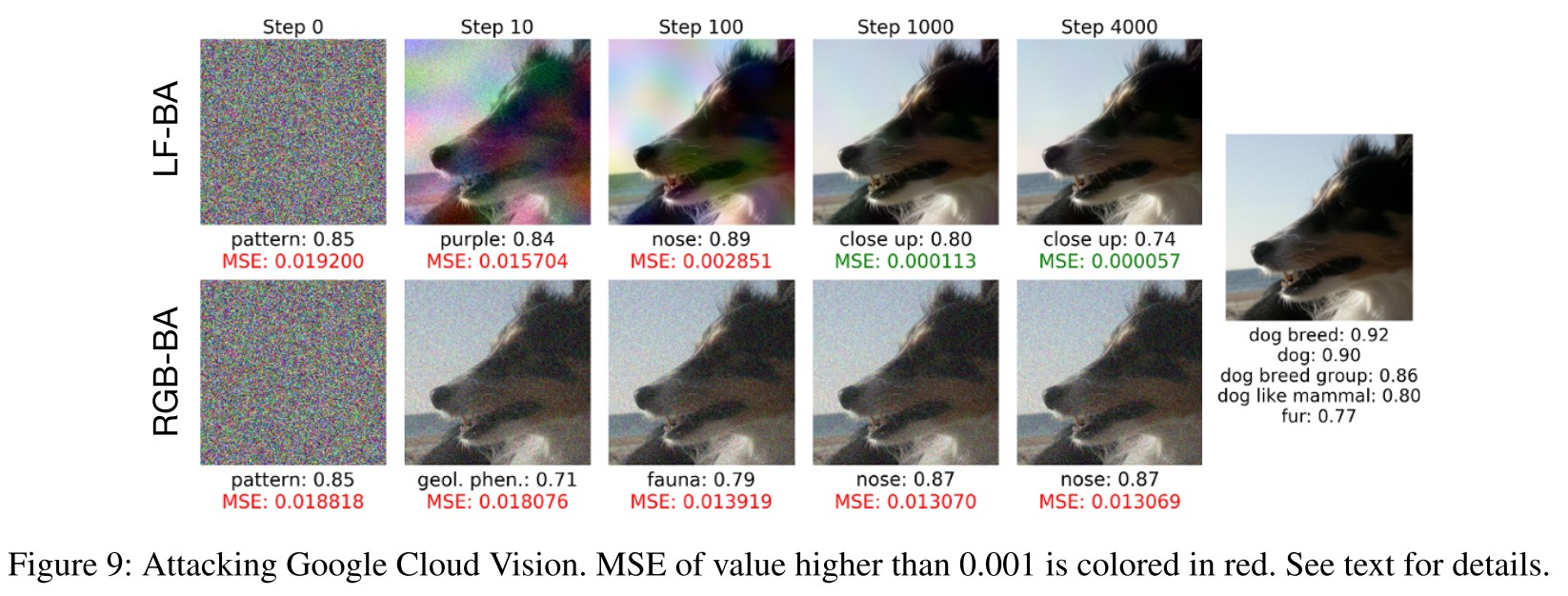
Inspirations

Although this paper packs up many experiments to demonstrate the efficiency of searching adversarial examples in low-frequency domain, I think its value lies more in developing a plausible low frequency gradient descent with a very simple implementation.

I think it's possible to use this for adversarial training, and there may be surprises.

On the Effectiveness of Low Frequency Perturbations - IJCAI 2019

Yash Sharma, Gavin Weiguang Ding, Marcus Brubaker. On the Effectiveness of Low Frequency Perturbations. IJCAI 2019. arXiv:1903.00073

Recent work demonstrates that restricting the search space in low frequency components improves adversarial attack, here they empirically study the effect of low frequency perturbations, and find that:

The benefit is not brought by the dimensional reduction.
The adversarially trained models are similarly vulnerable to low frequency perturbations as those undefended models.
$\ell_{\infty}\epsilon=16/255$ , the low frequency perturbations are perceptible.

The questions they pose are as follows:

Is the effectiveness of low frequency perturbations simply due to the reduced search space or specifically due to the use of low frequency components?
Under what conditions are low frequency perturbations more effective than unconstrained perturbations?

Testing against state-of-the-art ImageNet [Deng et al., 2009] defense methods, we show that, when perturbations are constrained to the low frequency subspace, they are 1) generated faster; and are 2) more transferable.

Frequency Constraints

$\delta$ $m\in\{0,1\}^{d\times d}$ $DCT(\delta)$ $IDCT$ on the masked DCT transform, i.e.

FreqMask(\delta)=IDCT(Mask(DCT(\delta)))

The following gradient is then used to conduct attacks:

\nabla_{\delta}J(x+FreqMask(\delta),y)

They choose four masks as shown in Figure 1 to study this problem.

Experiments

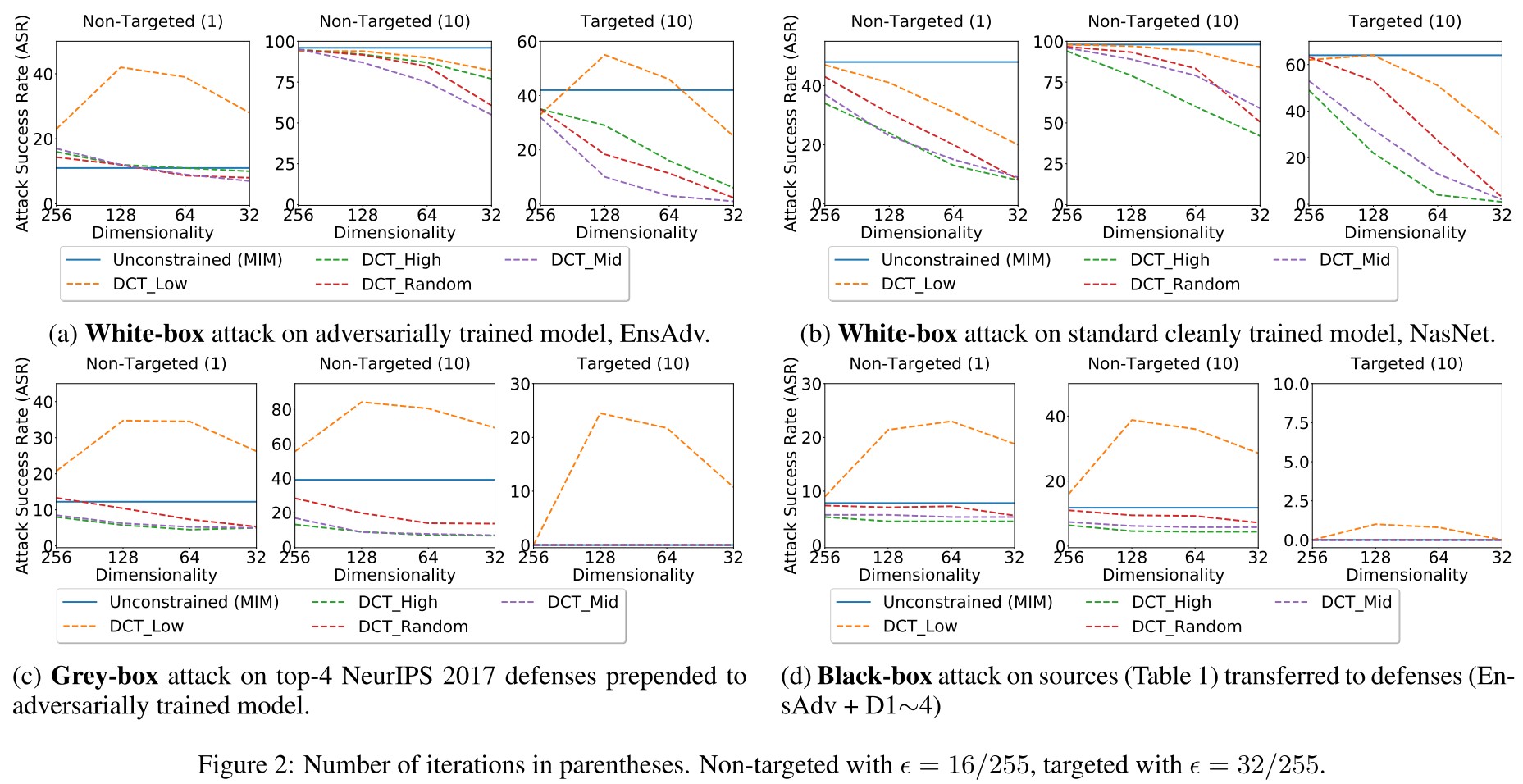
In each figure, the plots are, from left to right, non-targeted attack with iterations = 1, non-targeted with iterations = 10, and targeted with iterations = 10.

As shown in Figure 2, the effectiveness of low frequency perturbations are not brought by the reduced search space, but by the low frequency regime it uses.

Their other conclusions are as follows:

DCT Low generates effective perturbations faster on adversarially trained models, but not on cleanly trained models.
DCT Low bypasses defenses prepended to the adversarially trained model.
DCT Low helps black-box transfer to defended models.
DCT Low is not effective when transferring between undefended cleanly trained models.

It has been demonstrated later than this paper that adversarial training biases the robustness improvement to high frequency components, making the first three findings explainable. The fourth seems to indicate that standardly trained models have a favor to high frequency components.

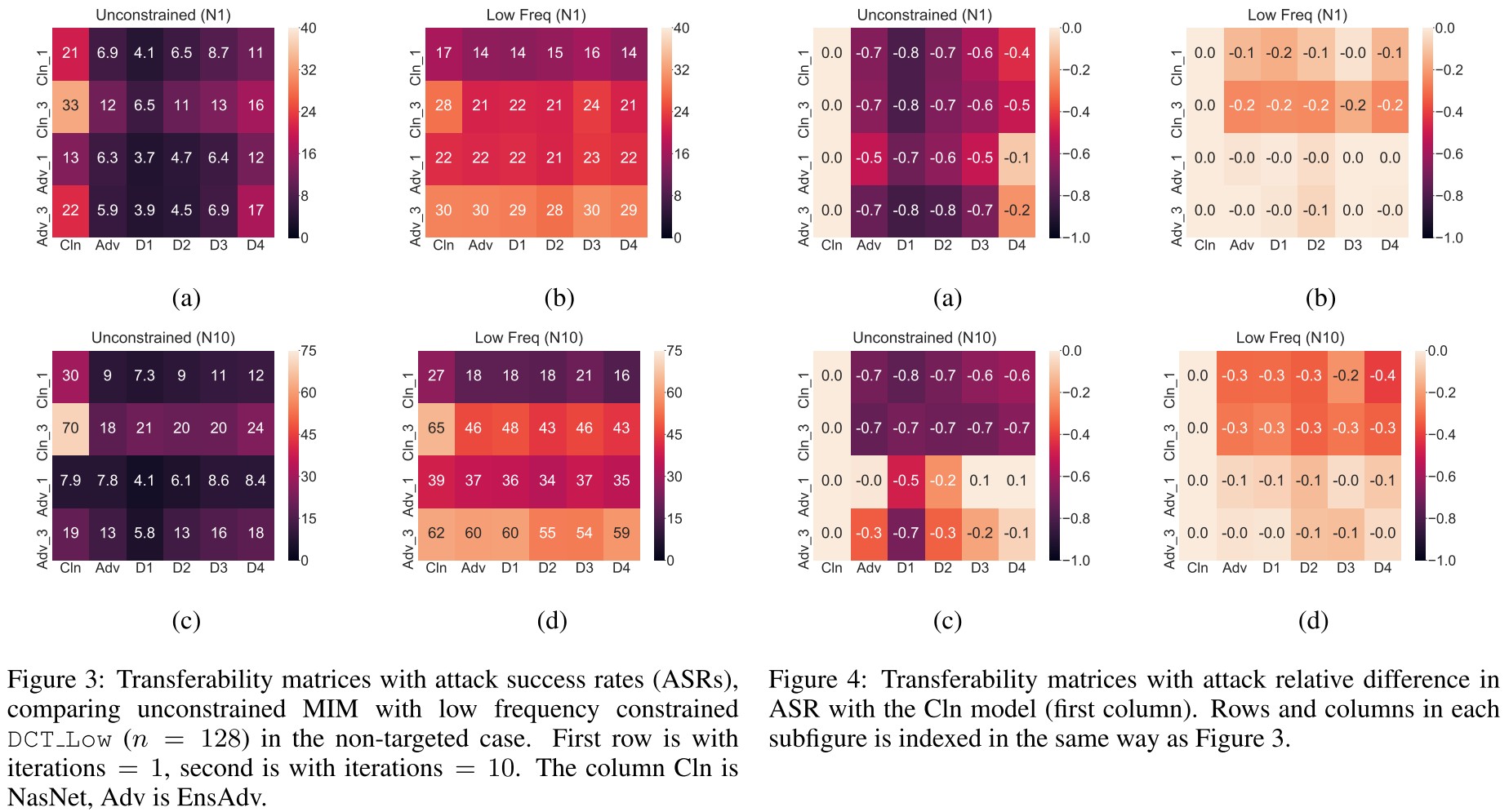
As shown in Figure 4,

Thus, as discussed, defended models are roughly as vulnerable as undefended models when encountered by low frequency perturbations.

They also test on adversarially trained model for CIFAR-10.

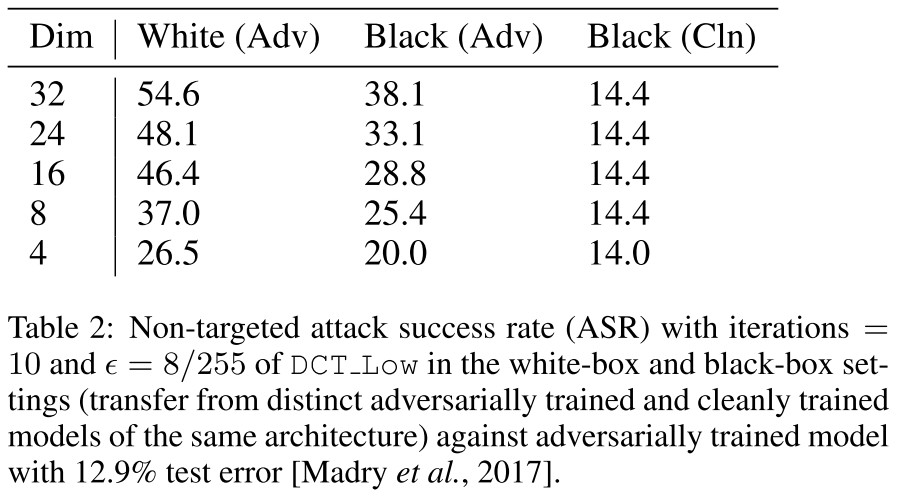
We observe that dimensionality reduction only hurts performance.

This table is a little ambeguous, and it's also not detailed in the original paper.

$\ell_{\infty}$ $\epsilon=16/255$ $\ell_{p}$ -norm metrics for measuring the misalignment between human and machine perception.

Inspirations

This is an empirical work of not very much novelty, they demonstrate that low frequency perturbations do not gain its effectiveness by reduction of search space and adversarially trained models are equally sensitive to low frequency perturbations as standard models.

I think there will be some work incorporating low frequency perturbations into adversarial training.