Support Vector Machine (SVM)

By LI Haoyang 2020.10.25

This is a short note summarized from Section 2.3, Chapter 2 in the book below

Bennamoun M, Shah SAA, Khan S, Rahmani H. A Guide to Convolutional Neural Networks for Computer Vision. Morgan & Claypool Publishers: Morgan & Claypool Publishers; 2018.

Support Vector Machine (SVM) is designed to find an optimal linear hyperplane to separate the training dataset into two classes, which is achieved by making the margin between the nearest data points to be as large as possible.

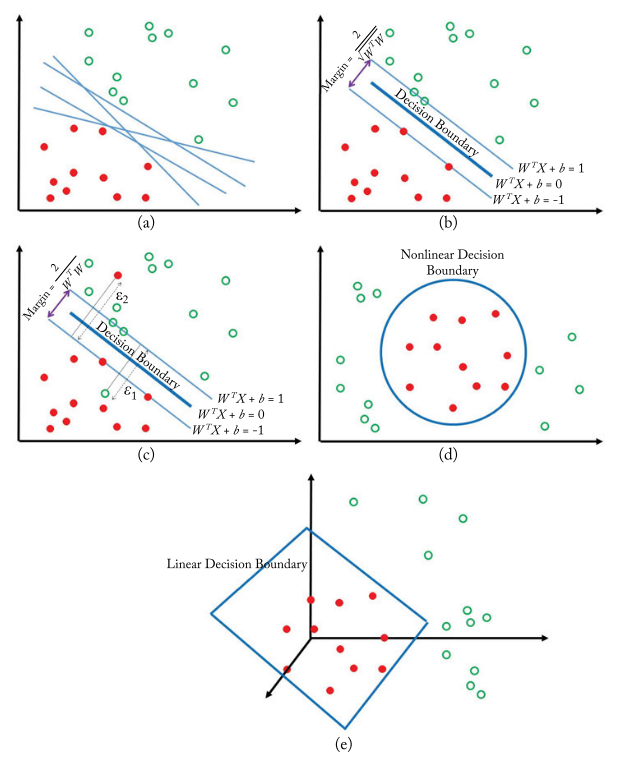
Given a training dataset $\cal{D}$ of two classes, i.e.

The hyperplane separating the data can be written as

Any data points above the hyperplane that suffice $\bold{w}^\top\bold{x}_i+b>0$ should be labeled $1$ and those below the hyperplane, i.e. that suffice $\bold{w}^\top\bold{x}_i+b < 0$ should be labeled $-1$. The nearest data points are divided by two hyperplanes, i.e. $\bold{w}^\top\bold{x}_i+b=1$ and $\bold{w}^\top\bold{x}_i+b=-1$, which have the distance of $\frac{2}{\sqrt{\bold{w}^\top\bold{w}}}$.

Thus, SVM is learned by solving the following problem

In the case when the data points are not completely separable, using a slack variables $\xi_i$ can allow some data points to appear on the other side (soft-margin extension)

In the case when the data points are not linearly separable, a projection $\phi:\R^d\to\R^D$ can be applied to project the data points into a higher-dimensional and linear separable space (nonlinear decison boundary)

In the case when $D\gg d$, there will be too many parameters to learn for $\bold{w}$ directly, to avoid which, the Lagrange dual form is used (dual form of SVM)

The derivation of dual form of SVM

For the original problem, the Lagrange function is

$$L(\bold{w},b,\alpha)=\frac{\bold{w}^\top\bold{w}}{2}-\sum_{i=1}^n\alpha_i[y_i(\bold{w}^\top\phi(\bold{x}_i)+b)-1]$$

By Lagrange duality, the following problem is equal to the original problem

$$\min_{\bold{w},b}\max_{\alpha}L(\bold{w},b,\alpha)\iff \max_{\alpha}\min_{\bold{w},b}L(\bold{w},b,\alpha)$$

The dual form of SVM is then

$$\min_{\bold{w},b}L(\bold{w},b,\alpha)$$

The derivativs of $L(\bold{w},b,\alpha)$ with respect to $\bold{w}$ and $b$ are

$$\nabla_{\bold{w}}L(\bold{w},b,\alpha)=\bold{w}-\sum_{i=1}^n\alpha_iy_i\phi(\bold{x}_i)\\ \nabla_bL(\bold{w},b,\alpha)=-\sum_{i=1}^n\alpha_iy_i$$

Thus the solution for the inner minimization is

$$\bold{w}=\sum_{i=1}^n\alpha_iy_i\phi(\bold{x}_i)\\ \sum_{i=1}^n\alpha_iy_i=0$$

Hence there is the dual form is SVM introduced above.

The calculation of $\phi(\bold{x}_i)^\top\phi(\bold{x}_i)$ can be intractable since it projects $\bold{x}_i$ to a higher-dimension, sometimes a very high dimension. Some kernel functions, e.g. linear, polynomial, Gaussian, Radial Basis Function (RBF), are equivalent to $\phi(\bold{x}_i)^\top\phi(\bold{x}_i)$, with which, the problem becomes (kernel trick)

Thus the final form of SVM.