The Channel in Convolutional Neural Nets

THOUGHTS

By LI Haoyang 2020.12.24

Content

Definitions

Channel

Reference: https://en.wikipedia.org/wiki/Channel_(digital_image)

For a digital image, a channel is the grayscale image of the same size as a color image, made of just one of these primary colors.

A general colored image often has three channels for red, green and blue respectively. A grayscale image only has one channel representing the intensity of pixels.

A channel is a projection of image in a color space.

Convolution

Reference: https://pytorch.org/docs/master/generated/torch.nn.Conv2d.html#torch.nn.Conv2d

The "convolution" operation used in convolutional neural networks is actually cross-correlation operation, not a real convolution as used in signal processing.

Taken from PyTorch document for torch.nn.Conv2d, it is defined as

where $*$ is cross-correlation operation, the input is a tensor of size $(N,C_{in},H,W)$, the output is a tensor of size $(N,C_{out},H_{out},W_{out})$ and the weight is a tensor of size $(C_{out}, C_{in},H_{weight}, W_{weight})$.

In this context, the input has $C_{in}$ channels and the output has $C_{out}$ channels. Each channel of the $C_{out}$ output channels is a sum of $C_{in}$ cross-correlations of corresponding channels of weight and input, shifted by a bias.

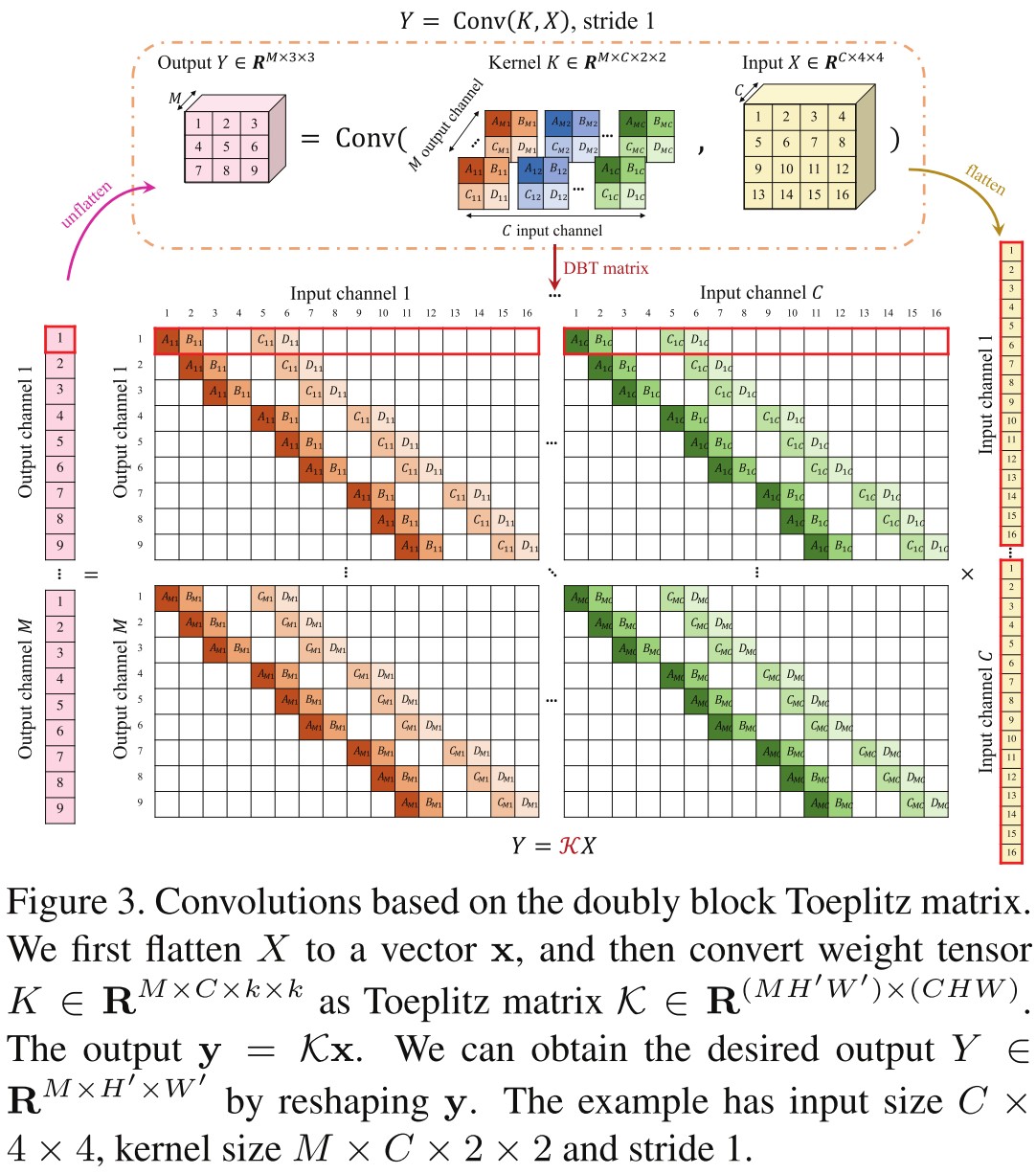
The convolution can be expanded into a linear operation between the flattened input and a corresponding Toeplitz matrix as shwon above¹. After flattening, a channel of the output $Y$ is obtained through a linear transform from the input $X$, i.e.

Convolution/Cross-correlation operation is linear.

Pooling

Reference: https://pytorch.org/docs/master/generated/torch.nn.AvgPool2d.html?highlight=avgpool2d#torch.nn.AvgPool2d

Taken from PyTorch document for torch.nn.AvgPool2d, it is defined as (one stride pooling):

where the kernel size is $(kH,kW)$, the input size is $(N,C,H,W)$ and the output size is $(N,C,H_{out},W_{out}), H_out=H/k,W_{out}=W/k$.

Other poolings are defined similarly.

It's obvious that pooling operation will not change the number of channels, but the dimension of each channel.

Average pooling is linear while others may be non-linear.

Activation

Reference: https://pytorch.org/docs/master/generated/torch.nn.ReLU.html?highlight=relu#torch.nn.ReLU

Activation is used to introduce non-linearity into neural networks. An activation function is an element-wise operation that only changes the intensity of each dimension.

Taken from PyTorch document for torch.nn.ReLU, it is defined as:

Other popular activation functions include:

• Sigmoid torch.nn.Sigmoid

  $$Sigmoid(x)=\sigma(x)=\frac{1}{1+\exp(-x)}$$

• Tanh torch.nn.Tanh

  $$Tanh(x)=tanh(x)=\frac{\exp(x)-\exp(-x)}{\exp(x)+\exp(-x)}$$

Activation is designed to be non-linear.

Convolutional Neural Networks

Reference: https://en.wikipedia.org/wiki/Convolutional_neural_network

In deep learning, a convolutional neural network (CNN, or ConvNet) is a class of deep neural networks, most commonly applied to analyzing visual imagery.[1] They are also known as shift invariant or space invariant artificial neural networks (SIANN), based on their shared-weights architecture and translation invariance characteristics.[2][3]

A typical convolutional neural network consists of multiple cascaded structure of convolutional layer, activation layer and pooling layer.

The Bound of Channel Number

Linear Algebra Perspective

Put activation layer aside, assuming there is a convolutional layer and an average layer, since these two layers are both linear, the output of these two layers is a linear projection of the input.

From this perspective, a channel of the output is a linear projection of the input, i.e. for an instance of input $X\in\R^{C\times H\times W}$, a channel of the output $y\in\R^{H^\prime\times W^\prime}$ is

where $A$ and $b$ are the coefficients of this linear projection.

From linear algebra, we know that if we want to accurately calculate a point of dimension $C\times H\times W$, we need exactly $C\times H\times W$ linearly independent equations.

With each channel of the output, we have $H^\prime\times W^\prime$ equations about the input, therefore, to recovery of the input, we need $C^\prime$ channels such that

where $M$ is the number of linearly correlated equations reconstructed from the output.

For a space of $C\times H\times W$ dimension, we only need at most $C\times H\times W$ one dimensional basis to represent every point in this space, as long as all of them are linearly independent.

An output of $C^\prime$ channels can be viewed as a point represented by the projections of the original data point from the higher dimension space to $C^\prime$ different directions, corresponding to $C^\prime$ different basis.

Since we need $C\times H\times W$ projections to one dimension to represent the original input of $C\times H\times W$ dimension, for projections to $H^\prime\times W^\prime$ dimension, the number of projections $C^\prime$ we need should suffice

Combining both, there should be

But it may be completely different if we consider the non-linear activation layer.

A non-linear activation will make some originally correlated equations non-correlated, intuitively, the $M$ will be drastically reduced if we take activation layer into consideration.

Information Theory Perspective

From a higher perspective, the information contained in an instance of input $X\in\R^{C\times H\times W}$ suffices that

For a corresponding output $Y\in\R^{C^\prime\times H^\prime\times W^\prime}$, the information contained suffices that

If we wish the network to be capable of preserving all possible information, it at least should suffice that

From this perspective, for data with less information, the number of channels can be drastically reduced proportionally.

This bound is intuitively super loose, since no data reaches the information upper bound; but in the other hand, no output reaches the information upper bound either, perhaps together they make the bound proper.

Signal Processing Perspective

According to Nyquist-Shannon Sampling Theorem, if we want to be capable of recovering the original signal without alias, the sampling frequency should be at least twice of the highest frequency of the original signal.

Although it was originally proposed for discretization of analog signal, most of the networks are designed such that every four times reduction of feature size is accompanied with a double of channel number.

From this perspective, to make the network capable of recovering the input, the channel number $C^\prime$ should suffice

This seems to be the most popular perspective.

Conflicts

The first two perspective seem to give the same bound, but the third perspective seems to differ from other two. Which one should we take?

It's a consensus that images are highly redundant, therefore with much fewer channels, even lower than the bound can still achieve competitive results. If we want to decide the channels we should adopt, the ultimate way seems to be measuring how redundant the images are by information.

Personally, I take the information theory perspective.